Da wir messen wollen, brauchen wir ein Maß für den Abstand zweier beliebiger Punkte
und
. Wir führen deshalb im dreidimensionalen Raum ein Abstandsmaß ein, und zwar nach Pythagoras die Wurzel aus den Quadraten der Koordinatendifferenzen:
Speziell ist der Abstand des Punktes
vom Nullpunkt
damit
.
|
Aufgabe 9.1: Abstände zwischen Punkten Berechnen Sie den Abstand der Punkte
|
und
voneinander sowie deren Abstände vom Nullpunkt. Die Mathematiker nennen den Raum mit dieser Abstandsdefinition euklidisch. Für den Abstand zweier verschiedener Punkte
gilt dann immer
, der Abstand eines Punktes von sich selbst verschwindet:
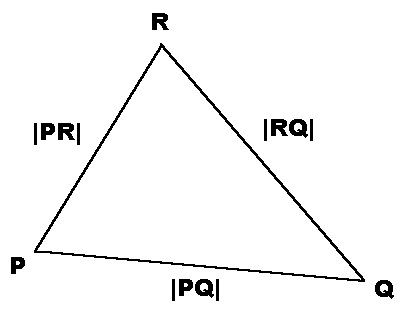
, und es gilt wie gewohnt die Dreiecksungleichung, die besagt, dass die Summe zweier Seitenlängen in jedem Dreieck größer ist als die Länge der dritten Seite:
zwischen Punkten
bzw.
kann man selbstverständlich entscheiden, welcher der größere ist, da es sich um reelle Zahlen handelt, die auf der Zahlengeraden angeordnet sind; die Punkte des
aber selbst sind wie schon die komplexen Zahlen nicht mehr anordenbar.