Wir bezeichnen eine Verschiebung dann als Vektor 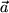 (oder gelegentlich auch als Tensor erster Stufe), wenn wir von der speziellen Anfangs- und Endlage der einzelnen Punkte eines verschobenen Gegenstands absehen, wenn uns nur die "Verschiebung an sich", d.h. der Betrag der Verschiebungsstrecke und die Richtung interessieren, ganz gleichgültig, wo im Raum die Verschiebung stattfindet.
(oder gelegentlich auch als Tensor erster Stufe), wenn wir von der speziellen Anfangs- und Endlage der einzelnen Punkte eines verschobenen Gegenstands absehen, wenn uns nur die "Verschiebung an sich", d.h. der Betrag der Verschiebungsstrecke und die Richtung interessieren, ganz gleichgültig, wo im Raum die Verschiebung stattfindet.
Wegen der in der Physik durchweg vorausgesetzten Homogenität des dreidimensionalen Raumes ist diese Begriffsbildung vorteilhaft für die Formulierung der Allgemeingültigkeit der physikalischen Gesetze. Sie bedeutet mathematisch, dass wir ähnlich wie bei der Einführung der rationalen Zahlen, wo wir z.B. 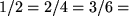 ... gleichgesetzt haben, die Verschiebungen in Äquivalenzklassen einteilen und alle Verschiebungen mit gleichem Betrag und gleicher Richtung identifizieren. Zur Veranschaulichung können wir dann wenn nötig einen beliebigen Repräsentanten der Klasse auswählen, z.B. den sogenannten Ortsvektor, indem wir die Verschiebung auf den Ursprung anwenden.
... gleichgesetzt haben, die Verschiebungen in Äquivalenzklassen einteilen und alle Verschiebungen mit gleichem Betrag und gleicher Richtung identifizieren. Zur Veranschaulichung können wir dann wenn nötig einen beliebigen Repräsentanten der Klasse auswählen, z.B. den sogenannten Ortsvektor, indem wir die Verschiebung auf den Ursprung anwenden.
Nachdem wir im dreidimensionalen euklidischen Raum bereits ein kartesisches Koordinatensystem zur Beschreibung der Punkte durch ihre Koordinaten eingeführt haben, erhebt sich die Frage nach der Charakterisierung der Vektoren in diesem System der drei paarweise orthogonalen Koordinatenachsen. Dazu wählen wir willkürlich für den Repräsentanten unseres (durch einen kleinen Pfeil darüber gekennzeichneten) Vektors 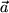 einen Anfangspunkt
einen Anfangspunkt 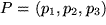 , verschieben diesen um die Strecke der Länge
, verschieben diesen um die Strecke der Länge  in die vorgeschriebene Richtung und gelangen so zum Endpunkt
in die vorgeschriebene Richtung und gelangen so zum Endpunkt 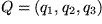 und mit dem folgenden Bild zu:
und mit dem folgenden Bild zu:
Vektor:
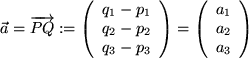
(Außer den hier verwendeten kleinen Pfeilen über den lateinischen Buchstaben bzw. über den beiden Punkten des Repräsentanten sind auch noch unterstrichene kleine Buchstaben, fett gedruckte Buchstaben oder deutsche Buchstaben übliche Bezeichnungen.)
Im Gegensatz zu einer durch sechs reelle Zahlen bestimmten speziellen Verschiebung eines bestimmten Punktes wird also ein Vektor nur durch drei reelle Zahlen charakterisiert. Zur Unterscheidung von den drei reellen Koordinaten eines Punktes nennt man diese
Vektorkomponenten:
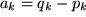
,
setzt sie jedoch wie die Punktkoordinaten in runde Klammern. Zur Unterscheidung schreibt man die Komponenten aber meist (wie oben) als Spalte untereinander statt hintereinander. Wenn man Wert darauf legt, die Vektorkomponenten wie die Punktkoordinaten hintereinander geschrieben zu haben, sollte man einen oberen Index " T " anfügen, als Abkürzung für "transponiert", d.h. umgelegt.
Transponierter Vektor:
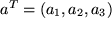
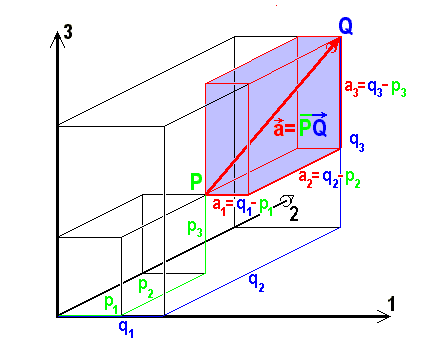
Wie man aus dem Bild sieht, sind die drei Komponenten eines Vektors die Längen der drei Projektionen des Repräsentanten 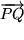 auf die Koordinatenachsen oder auch die Koordinaten des Endpunktes
auf die Koordinatenachsen oder auch die Koordinaten des Endpunktes 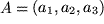 , den man durch die Verschiebung erreicht, wenn man als Anfangspunkt den Ursprung, also den Ortsvektor als Repräsentanten gewählt hat:
, den man durch die Verschiebung erreicht, wenn man als Anfangspunkt den Ursprung, also den Ortsvektor als Repräsentanten gewählt hat: 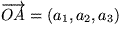 . Bei der Verwendung dieser speziellen Repräsentanten wird unmittelbar klar, dass es eine umkehrbar eindeutige Zuordnung zwischen der Gesamtheit der Punkte des
. Bei der Verwendung dieser speziellen Repräsentanten wird unmittelbar klar, dass es eine umkehrbar eindeutige Zuordnung zwischen der Gesamtheit der Punkte des 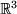 und der Menge aller Vektoren des sogenannten Vektorraums gibt. Die Mathematiker nennen das einen Isomorphismus.
und der Menge aller Vektoren des sogenannten Vektorraums gibt. Die Mathematiker nennen das einen Isomorphismus.
Genauso wie durch den Betrag und die zwei Richtungswinkel ist ein Vektor durch seine drei Komponenten eindeutig charakterisiert, d.h. eine Vektorgleichung bedeutet drei Gleichungen für die einzelnen Komponenten, was an der Vektorschreibweise besonders geschätzt wird:
Vektorgleichung:
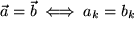
für
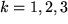
Der Betrag der Verschiebungsstrecke, d.h. die Länge eines Vektors ergibt sich aus seinen Komponenten nach Pythagoras wie früher der Abstand zweier Punkte aus den Koordinatendifferenzen:
Länge:
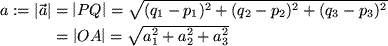
|
Aufgaben 9.5: Länge von Vektoren
Bestimmen Sie die Länge folgender Vektoren: 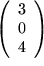 Lösung und Lösung und  . Lösung . Lösung
|
Um uns die charakteristischen Unterschiede ganz klar zu machen, die trotz des Isomorphismus zwischen den Komponenten eines Vektors  und den Koordinaten des Endpunkts
und den Koordinaten des Endpunkts 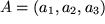 des repräsentierenden Ortsvektors bestehen, und an die uns die verschiedenen Schreibweisen immer wieder erinnern sollen, untersuchen wir erneut wie früher, was mit den Komponenten geschieht, bei Transformationen des Koordinatensystems:
des repräsentierenden Ortsvektors bestehen, und an die uns die verschiedenen Schreibweisen immer wieder erinnern sollen, untersuchen wir erneut wie früher, was mit den Komponenten geschieht, bei Transformationen des Koordinatensystems:
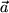 (oder gelegentlich auch als Tensor erster Stufe), wenn wir von der speziellen Anfangs- und Endlage der einzelnen Punkte eines verschobenen Gegenstands absehen, wenn uns nur die "Verschiebung an sich", d.h. der Betrag der Verschiebungsstrecke und die Richtung interessieren, ganz gleichgültig, wo im Raum die Verschiebung stattfindet.
(oder gelegentlich auch als Tensor erster Stufe), wenn wir von der speziellen Anfangs- und Endlage der einzelnen Punkte eines verschobenen Gegenstands absehen, wenn uns nur die "Verschiebung an sich", d.h. der Betrag der Verschiebungsstrecke und die Richtung interessieren, ganz gleichgültig, wo im Raum die Verschiebung stattfindet.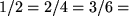 ... gleichgesetzt haben, die Verschiebungen in Äquivalenzklassen einteilen und alle Verschiebungen mit gleichem Betrag und gleicher Richtung identifizieren. Zur Veranschaulichung können wir dann wenn nötig einen beliebigen Repräsentanten der Klasse auswählen, z.B. den sogenannten Ortsvektor, indem wir die Verschiebung auf den Ursprung anwenden.
... gleichgesetzt haben, die Verschiebungen in Äquivalenzklassen einteilen und alle Verschiebungen mit gleichem Betrag und gleicher Richtung identifizieren. Zur Veranschaulichung können wir dann wenn nötig einen beliebigen Repräsentanten der Klasse auswählen, z.B. den sogenannten Ortsvektor, indem wir die Verschiebung auf den Ursprung anwenden.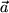 einen Anfangspunkt
einen Anfangspunkt 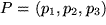 , verschieben diesen um die Strecke der Länge
, verschieben diesen um die Strecke der Länge  in die vorgeschriebene Richtung und gelangen so zum Endpunkt
in die vorgeschriebene Richtung und gelangen so zum Endpunkt 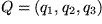 und mit dem folgenden Bild zu:
und mit dem folgenden Bild zu: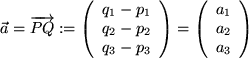
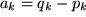 ,
,
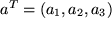
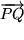 auf die Koordinatenachsen oder auch die Koordinaten des Endpunktes
auf die Koordinatenachsen oder auch die Koordinaten des Endpunktes 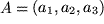 , den man durch die Verschiebung erreicht, wenn man als Anfangspunkt den Ursprung, also den Ortsvektor als Repräsentanten gewählt hat:
, den man durch die Verschiebung erreicht, wenn man als Anfangspunkt den Ursprung, also den Ortsvektor als Repräsentanten gewählt hat: 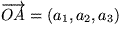 . Bei der Verwendung dieser speziellen Repräsentanten wird unmittelbar klar, dass es eine umkehrbar eindeutige Zuordnung zwischen der Gesamtheit der Punkte des
. Bei der Verwendung dieser speziellen Repräsentanten wird unmittelbar klar, dass es eine umkehrbar eindeutige Zuordnung zwischen der Gesamtheit der Punkte des 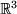 und der Menge aller Vektoren des sogenannten Vektorraums gibt. Die Mathematiker nennen das einen Isomorphismus.
und der Menge aller Vektoren des sogenannten Vektorraums gibt. Die Mathematiker nennen das einen Isomorphismus.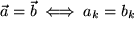 für
für 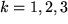
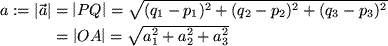
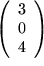
 .
.  und den Koordinaten des Endpunkts
und den Koordinaten des Endpunkts 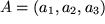 des repräsentierenden Ortsvektors bestehen, und an die uns die verschiedenen Schreibweisen immer wieder erinnern sollen, untersuchen wir erneut wie früher, was mit den Komponenten geschieht, bei Transformationen des Koordinatensystems:
des repräsentierenden Ortsvektors bestehen, und an die uns die verschiedenen Schreibweisen immer wieder erinnern sollen, untersuchen wir erneut wie früher, was mit den Komponenten geschieht, bei Transformationen des Koordinatensystems: