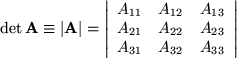
Determinanten:

Das wichtigste Charakteristikum einer Matrix ist ihre Determinante. Für diese sind folgende Bezeichnungen gebräuchlich:

Determinante:

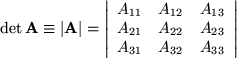
Leibniz gab folgende

Das ergibt eine reelle Zahl, nämlich die Summe bzw. Differenz aus Produkten von jeweils drei Elementen der Matrix. Die (linken) Zeilenindizes lauten bei allen Termen immer , die (rechten) Spaltenindizes durchlaufen dagegen alle Permutationen dieser drei Zahlen: , , ; , , . Das Vorzeichen der einzelnen Terme wird dabei durch die Anzahl der Transpositionen (:Vertauschungen je zweier Indizes) bestimmt, die benötigt werden, um aus der Konfiguration die betreffende Konfiguration zu erhalten. Die ersten drei der oben angegebenen Konfigurationen erhält man durch eine gerade Anzahl von Transpositionen, sie erhalten ein Pluszeichen, die restlichen drei, durch eine ungerade Zahl von Vertauschungen erhaltenen, werden subtrahiert: z.B. zu (ungerade), aber zu (gerade), ....
Bei -Matrizen erhält man sechs Summanden, bei diesen sind die geraden Permutationen auch durch zyklische Permutation zu finden.

Neben dieser ganz allgemein gültigen Definition gibt es zur Berechnung der Determinate einer Matrix mehrere verschiedene Methoden. Wir wollen zwei davon kennenlernen und betrachten zunächst die speziell für Determinanten von -Matrizen geltende Sarrussche Regel:

Dazu schreiben wir die erste und zweite Spalte der Matrix noch einmal rechts neben unsere zu bestimmende Determinante:

zur Sarrus-Regel:

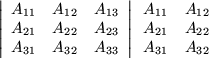
In dieser Anordnung multiplizieren wir die Elemente in der Hauptdiagonale miteinander, addieren dazu das Produkt der rechts daneben in Hauptdiagonalenrichtung stehenden Elemente und . Davon subtrahieren wir das Produkt der Elemente in der Nebendiagonale und ebenfalls zwei Mal die Produkte der jeweils rechts daneben in Nebendiagonalenrichtung angeordneten drei Matrixelemente und . Damit erhalten wir die gewünschte Determinante.

Häufig führt eine weitere Methode noch schneller zum Ziel, die sogenannte Entwicklung nach der ersten Zeile: Da es sich dabei um eine sukzessive Methode handelt, machen wir uns zuerst klar, dass die Determinante einer -Matrix aus dem Produkt der beiden Diagonalelemente vermindert um das Produkt der Nebendiagonalelemente besteht. Nach Wegstreichen der dritten Zeile und der dritten Spalte unserer gesuchten -Determinaten bleibt diese -Determinante gerade übrig. Man nennt sie Adjunkte und versieht sie mit den Indizes der weggestrichenen Reihen:

Adjunkte:

Mit Hilfe dieser Adjunkten läßt sich die gesuchte -Determinante folgendermaßen schreiben:

.

Wir werden sogleich sehen, dass die Beschränkung auf eine Entwicklung nach der ersten Zeile keine Einschränkung bedeutet, da die Determinante viele Symmetrieeigenschaften besitzt. Mit deren Hilfe kann man leicht auch Entwicklungen nach anderen Zeilen oder auch Spalten erhalten. Dabei verwenden wir den Begriff der

Um eine prägnante Schreibweise zu ermöglichen, fassen wir außerdem manchmal auch die übereinanderstehenden Matrixelemente zu sogenannten Spaltenvektoren zusammen, z.B.

mit Spaltenvektoren:

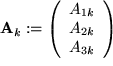
Die Determinanten haben eine Fülle von interessanten charakteristischen Symmetrieeigenschaften, die ihre Berechnung und den Umgang mit ihnen außerordentlich erleichtern.

Symmetrieeigenschaften der Determinaten:

a) Eine Determinante ist invariant gegenüber Transposition, d.h. Spiegelung an der Hauptdiagonalen:

b) Eine Determinante bleibt unverändert, wenn zu einer ihrer Reihen eine Linearkombination der anderen Reihen addiert wird, z.B.:

c) Eine Determinate ändert ihr Vorzeichen bei jeder Permutation zweier Reihen: z.B.

d) Die Determinanten sind reihenweise homogen: mit einer rellen Zahl

e) Eine Determinate verschwindet, falls die Reihenvektoren koplanar (: linear abhängig; siehe Abschnitt 9.4.4) sind oder einer der Reihenvektoren der Nullvektor ist:

f) Eine Determinante mit ungerader Dimensionszahl bleibt bei zyklischer Permutation der Reihen unverändert:

.

g) Eine Determinante mit ungerader Dimensionszahl verschwindet, falls die Matrix antisymmetrisch ist :

.

h) Die Determinaten sind additiv, falls die Summanden sich nur in einer Reihe unterscheiden: z.B.

.

i) Die Determinante des Produkts zweier Matrizen ist gleich dem Produkt der Determinanten der beiden Faktoren:

Aufgabe 9.12: Berechnen Sie folgende Determinaten: Lösung Lösung Lösung Lösung Lösung Lösung Lösung Lösung Lösung Lösung Lösung Lösung Lösung Lösung

Zurück zum Text