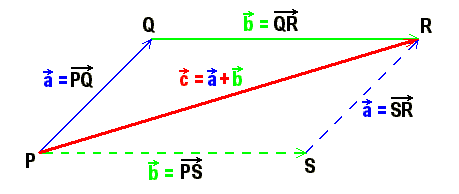
Während bei den Punkten des dreidimensionalen euklidischen Raumes von irgendwelchen Rechenoperationen nicht die Rede sein konnte, ist es vom physikalischen Standpunkt sehr sinnvoll, nach Rechenoperationen für Vektoren zu fragen: z.B. können mehrere Verschiebungen hintereinander ausgeführt werden: Nachdem wir einen Massenpunkt z.B. vom Punkt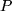 
gemäß dem Vektor 
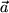zum Punkt 
verschoben haben, können wir ihn anschließend von entsprechend der Verschiebungsvorschrift des Vektors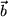 
zum Punkt 
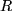weiterschieben. Wir hätten ersichtlich dieselbe Endlage erreicht, wenn wir ihn sofort in einem Zug von 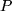nach 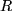geschoben hätten, gemäß einem Vektor 
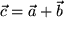, den wir als die Vektorsumme von 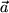und 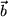bezeichnen:
für 
Die geometrische Addition der Vektoren erfolgt komponentenweise, bedeutet also die algebraische Addition der drei Komponenten. Daher stammt die Bezeichnung "Addition" für Vektoren.
