Insbesondere ist es immer möglich, schon nach zwei Verschiebungen wieder zum Ausganspunkt zurückzukehren: D.h. es existiert zu jedem Verschiebungsvektor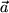 
wie bei den reellen Zahlen eine eindeutige Umkehrung, das Negative:
mit 
.
Dabei sind einfach Anfangs- und Endpunkt des Repräsentanten zu vertauschen: 
.
Mit dem Negativen der Vektoren wird analog wie bei den reellen Zahlen auch für die Vektoren eine Subtraktion definierbar, d.h.
mit 
.
Der Vektor 
mit den Komponenten 
für 
löst nämlich die obige Gleichung.
, 
; 
, 
; 
, 
; 
, 
; 
, 
; 
, 
.