A) Zunächst betrachten wir Linearkombinationen aus zwei verschiedenen Vektoren: 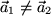 : Dabei können zwei Fälle auftreten:
: Dabei können zwei Fälle auftreten:
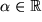 gibt, so dass
gibt, so dass 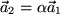 gilt oder anders ausgedrückt: in
gilt oder anders ausgedrückt: in  mindestens einer der Faktoren
mindestens einer der Faktoren 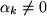 ist, z.B.
ist, z.B. 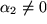 , so dass nach
, so dass nach 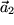 aufgelöst werden kann
aufgelöst werden kann 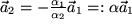 ,
,
so heißt das, dass 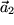 durch einen Vektor repräsentiert werden kann, der ganz auf der Geraden liegt, die durch
durch einen Vektor repräsentiert werden kann, der ganz auf der Geraden liegt, die durch 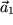 geht. Dann heißen die beiden Vektoren
geht. Dann heißen die beiden Vektoren 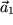 und
und 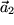 linear abhängig, speziell auch kollinear.
linear abhängig, speziell auch kollinear.
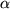 gibt, so dass
gibt, so dass 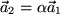 für alle
für alle 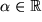 , also
, also  oder anders ausgedrückt:
oder anders ausgedrückt: 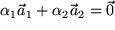 nur erreicht werden kann, wenn sowohl
nur erreicht werden kann, wenn sowohl  als auch
als auch 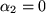 ,
,
dann spannen die beiden Vektoren 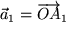 und
und 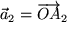 durch die drei Punkte
durch die drei Punkte 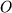 ,
, 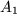 und
und  eine Ebene auf, und jeder Punkt dieser Ebene ist durch eine Linearkombination
eine Ebene auf, und jeder Punkt dieser Ebene ist durch eine Linearkombination 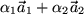 mit reellen Faktoren
mit reellen Faktoren 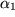 und
und 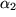 erreichbar.
erreichbar.
B) Dann untersuchen wir Linearkombinationen aus drei verschiedenen Vektoren: 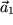 ,
, 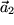 und
und 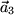 , wobei wieder zwei Fälle möglich sind:
, wobei wieder zwei Fälle möglich sind:
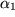 und
und 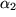 gefunden werden können, so dass
gefunden werden können, so dass 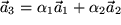 oder anders ausgedrückt: in
oder anders ausgedrückt: in 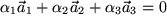 mindestens ein
mindestens ein 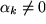 ist, z.B.
ist, z.B. 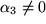 , so dass nach
, so dass nach 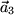 aufgelöst werden kann,
aufgelöst werden kann,
so heißt das wie eben gezeigt, dass 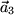 durch einen Vektor repräsentiert werden kann, der ganz in der von
durch einen Vektor repräsentiert werden kann, der ganz in der von 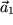 und
und 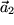 aufgespannten Ebene liegt. Dann nennt man die drei Vektoren
aufgespannten Ebene liegt. Dann nennt man die drei Vektoren 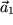 ,
, 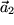 und
und 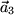 linear abhängig, speziell auch koplanar.
linear abhängig, speziell auch koplanar.
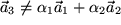 oder anders ausgedrückt
oder anders ausgedrückt 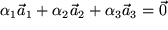 nur erreichbar ist, wenn alle drei
nur erreichbar ist, wenn alle drei 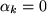 sind,
sind,
dann spannen die drei Vektoren 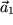 ,
, 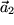 und
und 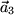 den ganzen
den ganzen 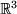 auf. Man sagt dann, sie bilden eine Basis des
auf. Man sagt dann, sie bilden eine Basis des 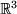 , d.h. jeder dreidimensionale Vektor ist als Linearkombination der drei Basisvektoren darstellbar:
, d.h. jeder dreidimensionale Vektor ist als Linearkombination der drei Basisvektoren darstellbar: 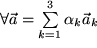 .
.
C) Vier Vektoren schließlich sind im 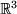 immer linear abhängig.
immer linear abhängig.
|
Aufgabe 9.17: Basisvektoren
|
Besonders bequem als Basis sind Einheitsvektoren.
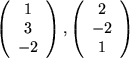 und
und 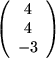 ?
? 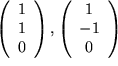 und
und 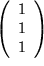 ?
?