Aktiver Standpunkt:
Wir haben uns bei unseren Tansformationsüberlegungen immer nur damit beschäftigt, wie die Koordinaten eines bestimmten Punktes oder die Komponenten eines festen Vektors aussehen würden, wenn wir das zur Beschreibung verwendete Koordinatensystem bzw. die Basisvektoren geändert hätten. Dabei wird ein und derselbe Vektor 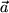 bezüglich zweier verschiedener Orthonormalbasen
bezüglich zweier verschiedener Orthonormalbasen 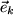 bzw.
bzw. 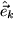 durch verschiedene Komponenten
durch verschiedene Komponenten 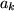 und
und 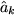 dargestellt:
dargestellt: 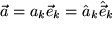 . Wenn dabei z.B.
. Wenn dabei z.B.  , also in positiver 3-Richtung gesehen um den Winkel
, also in positiver 3-Richtung gesehen um den Winkel 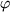 im Uhrzeigersinn um die 3-Achse gedreht würde, haben wir gesehen, dass auch die Komponenten
im Uhrzeigersinn um die 3-Achse gedreht würde, haben wir gesehen, dass auch die Komponenten 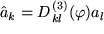 entsprechend gedreht werden. Man nennt dies den passiven Standpunkt und wir werden uns im ganzen Kurs konsequent immer auf diesen Standpunkt stellen. Dieses Problem ist deshalb wichtig, weil die Physiker darauf achten müssen, dass ihre Gesetze so formuliert werden, dass sie von der Wahl des Koordintensystems unabhängig sind.
entsprechend gedreht werden. Man nennt dies den passiven Standpunkt und wir werden uns im ganzen Kurs konsequent immer auf diesen Standpunkt stellen. Dieses Problem ist deshalb wichtig, weil die Physiker darauf achten müssen, dass ihre Gesetze so formuliert werden, dass sie von der Wahl des Koordintensystems unabhängig sind.
Die Physiker haben daneben aber noch ein zunächst ganz anderes Problem, nämlich die mathematische Beschreibung von Massenpunkten, Vektoren, usw., die sich tatsächlich im Raum (z.B. mit der Zeit) bewegen, etwa rotieren. Da müssen dann der ursprüngliche Vektor 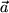 und der z.B. in positiver 3-Richtung gesehen um den Winkel
und der z.B. in positiver 3-Richtung gesehen um den Winkel 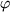 im Uhrzeigersinn um die 3-Achse gedrehte physikalische Vektor
im Uhrzeigersinn um die 3-Achse gedrehte physikalische Vektor 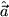 in ein und demselben Koordinatensystem
in ein und demselben Koordinatensystem 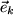 beschrieben werden:
beschrieben werden: 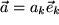 und
und 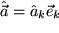 . Man nennt dies den aktiven Standpunkt. Das folgende Bild zeigt Ihnen, dass in diesem Fall gerade
. Man nennt dies den aktiven Standpunkt. Das folgende Bild zeigt Ihnen, dass in diesem Fall gerade 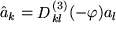 gilt.
gilt.
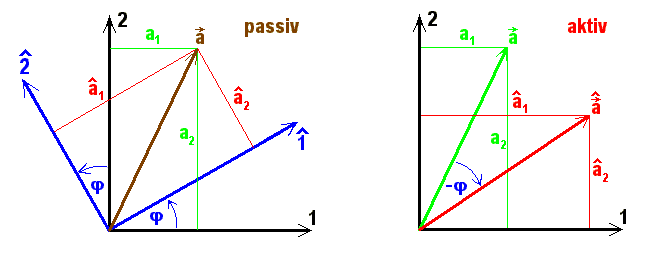
Bild 9.15: Unterschied zwischen passivem und aktivem Standpunkt
Wir haben dabei absichtlich in beiden Fällen das Dach zur Kennzeichnung der neuen Komponenten verwendet, um ganz deutlich zu machen, dass die Relation
zwei völlig verschiedene Bedeutungen haben kann, nämlich:
1.) die transformierten Komponenten eines Vektors 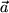 als Linearkombination der alten bei einer Drehung des Koordinatensystems um den Winkel
als Linearkombination der alten bei einer Drehung des Koordinatensystems um den Winkel 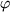 um die 3-Richtung und
um die 3-Richtung und
2.) die Komponenten eines Vektors nach seiner Drehung um den Winkel  um die 3-Richtung als Linearkombination seiner Komponenten vor der Drehung.
um die 3-Richtung als Linearkombination seiner Komponenten vor der Drehung.
Wenn man sich die verschiedenen Sachverhalte ein einziges Mal klargemacht hat, gibt es kaum mehr Gefahr für Verwirrung, sondern eher Freude über die Tatsache, dass man mit dem Studium derselben Drehmatrizen in einem Streich zwei Probleme lösen kann.
Zurück zum Text
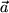 bezüglich zweier verschiedener Orthonormalbasen
bezüglich zweier verschiedener Orthonormalbasen 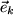 bzw.
bzw. 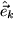 durch verschiedene Komponenten
durch verschiedene Komponenten 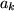 und
und 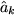 dargestellt:
dargestellt: 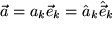 . Wenn dabei z.B.
. Wenn dabei z.B.  , also in positiver 3-Richtung gesehen um den Winkel
, also in positiver 3-Richtung gesehen um den Winkel 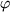 im Uhrzeigersinn um die 3-Achse gedreht würde, haben wir gesehen, dass auch die Komponenten
im Uhrzeigersinn um die 3-Achse gedreht würde, haben wir gesehen, dass auch die Komponenten 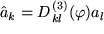 entsprechend gedreht werden. Man nennt dies den passiven Standpunkt und wir werden uns im ganzen Kurs konsequent immer auf diesen Standpunkt stellen. Dieses Problem ist deshalb wichtig, weil die Physiker darauf achten müssen, dass ihre Gesetze so formuliert werden, dass sie von der Wahl des Koordintensystems unabhängig sind.
entsprechend gedreht werden. Man nennt dies den passiven Standpunkt und wir werden uns im ganzen Kurs konsequent immer auf diesen Standpunkt stellen. Dieses Problem ist deshalb wichtig, weil die Physiker darauf achten müssen, dass ihre Gesetze so formuliert werden, dass sie von der Wahl des Koordintensystems unabhängig sind.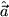 in ein und demselben Koordinatensystem
in ein und demselben Koordinatensystem 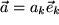 und
und 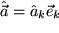 . Man nennt dies den aktiven Standpunkt. Das folgende Bild zeigt Ihnen, dass in diesem Fall gerade
. Man nennt dies den aktiven Standpunkt. Das folgende Bild zeigt Ihnen, dass in diesem Fall gerade 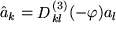 gilt.
gilt.
 um die 3-Richtung als Linearkombination seiner Komponenten vor der Drehung.
um die 3-Richtung als Linearkombination seiner Komponenten vor der Drehung.