Diese neun Gleichungen enthalten die gesamte Information über die Orthogonalität und die Normierung der Basisvektoren. Sie lassen sich zu einer einzigen Gleichung zusammenfassen,
Orthonormalität: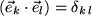 
,
,
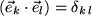wenn wir das nach Leopold Kronecker benannte Symbol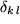 
zu Hilfe nehmen, das folgendermaßen definiert ist:
|
Kronecker-Symbol |
Wie das Skalarprodukt ist dieses Zahlenschema symmetrisch gegen Vertauschen der beiden Indizes: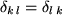 
. Im folgenden Bild ist das Zahlenschema in der Ebene bildlich dargestellt:
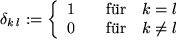
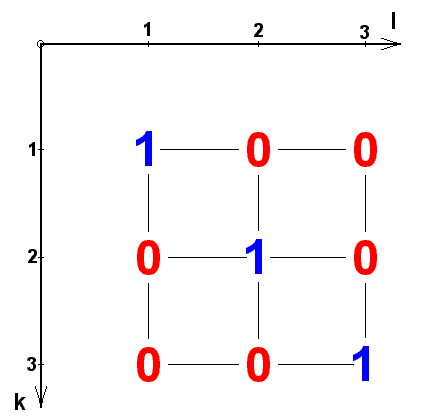
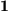gut erkennen kann. Gelegentlich brauchen wir die Summe der drei Diagonalelemente der Matrix, die man Spur nennt:
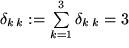(mit Einstein-Summenkonvention!)