Nun wollen wir sehen, wie man das Skalarprodukt berechnet, wenn die beiden Vektoren in Komponenten gegeben sind: 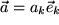 und
und 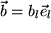 : (jeweils mit Summenkonvention!)
: (jeweils mit Summenkonvention!)
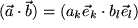 wobei sowohl über
wobei sowohl über 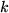 , als auch über
, als auch über  summiert wird
summiert wird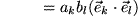 wegen der Homogenität des Skalarprodukts
wegen der Homogenität des Skalarprodukts wegen der Orthonormalität der Basisvektoren
wegen der Orthonormalität der Basisvektoren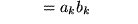 wegen des Kronecker-Symbols bleibt von der Summe über
wegen des Kronecker-Symbols bleibt von der Summe über  nur der Term
nur der Term 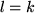 übrig. Deshalb bleibt nur noch die Summe über
übrig. Deshalb bleibt nur noch die Summe über 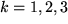 also
also

|
Aufgabe 9.26: Kronecker-Symbol Leiten Sie die obige Formel ausführlich her mit explizitem Ausmultiplizieren der Klammern |
|
Aufgabe 9.27: Orthonormalbasis Bilden die drei Vektoren |
Speziell für einen der drei Basisvektoren erhalten wir:
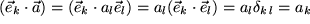
ausführlich mit Summenzeichen: 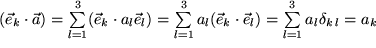 , die k-te Komponente des Vektors
, die k-te Komponente des Vektors 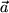 , denn die skalare Multiplikation mit dem k-ten Basisvektor ergibt ja die Projektion des Vektors auf die k-Achse. Daraus kann man leicht den gesamten Vektor
, denn die skalare Multiplikation mit dem k-ten Basisvektor ergibt ja die Projektion des Vektors auf die k-Achse. Daraus kann man leicht den gesamten Vektor 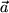 wieder zusammensetzen:
wieder zusammensetzen:
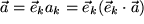
|
Aufgabe 9.28: Skalarprodukt Bestimmen Sie das Skalarprodukt und die Länge der Projektionen für die beiden Vektoren |
|
Aufgabe 9.29: Winkel mit den Koordinatenachsen: Welche Winkel bildet der Vektor |
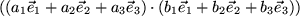 ohne Verwendung des Kronecker-Symbols, damit Sie ermessen können, welche Ersparnis an Rechenaufwand das Symbol mit sich bringt.
ohne Verwendung des Kronecker-Symbols, damit Sie ermessen können, welche Ersparnis an Rechenaufwand das Symbol mit sich bringt. 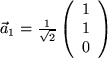 ,
, 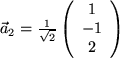 und
und 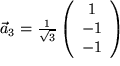 eine Orthonormalbasis des Vektorraums?
eine Orthonormalbasis des Vektorraums? 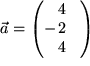 und
und 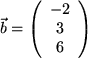
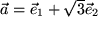 mit den Koordinatenachsen?
mit den Koordinatenachsen?