Wir haben nun ein kommutatives Produkt zweier Vektoren, zwar nur einen Skalar ohne Assoziativgesetz und eindeutiges Inverses, aber eine einfache und kurze Charakterisierung der Orthonormalität unserer Basisvektoren und vor allem eine angemessene und treffende Beschreibung all der vielen physikalischen Situationen, bei denen die Projektion eines Vektors auf einen anderen ein wichtige Rolle spielt.
Wir können uns jedoch damit nicht zufrieden geben, denn zum einen wollen wir grundsätzlich doch wenigstens versuchen, ein echtes Vektorprodukt zu finden, das zwei Vektoren wieder ein Element des Vektorraums zuordnet, zum anderen suchen wir eine einfache schöne Kennzeichnung der Tatsache, dass unsere Basisvektoren ein Rechtskoordinatensystem bilden und schließlich kennen wir in der Physik eine ganze Reihe von vektorartigen Größen, die nicht so einfach mit Verschiebungen in Zusammenhang gebracht werden können, wie etwa den Drehimpuls oder das Drehmoment, sondern mit Drehungen häufig von ausgedehnten starren Körpern zu tun haben, die um eine Achse drehbar gelagert sind. Die Existenz eines Vektorprodukts neben dem Skalarprodukt ist übrigens eine spezielle Eigenart des dreidimensionalen Raumes; bei den Vektoren im 
und 
gibt es so etwas nicht.
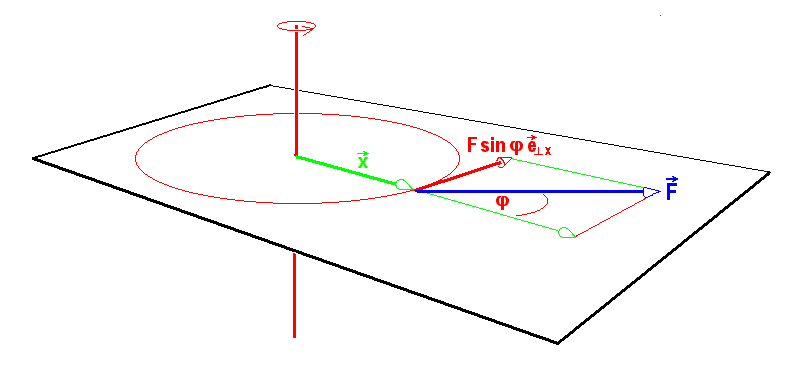
, die Projektion der Kraft senkrecht zur Verbindungslinie von Drehachse und Angriffspunkt der Kraft. Andererseits ist neben dem Verbindungsvektor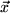 
vom Drehpunkt zum Ansatzpunkt der Kraft und dem Kraftvektor 
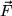selbst durch die Drehachse eine dritte Richtung im Raum ausgezeichnet, die immer senkrecht auf der von