Wir versuchen deshalb folgenden Ansatz als echte innere Verknüpfung zweier beliebiger Vektoren
und
:
|
Vektorprodukt:
|
Außer dem Sinus des eingeschlossenen Winkels und den Längen der beiden Vektoren haben wir den
Einheitsvektor
dazugenommen, der senkrecht auf der von den beiden Vektoren aufgespannten Ebene steht und mit den Vektoren
und
(in dieser Reihenfolge!) eine Rechtsschraube bildet.
Zur deutlichen Unterscheidung vom Skalarprodukt verwenden wir als Malzeichen ein Kreuz
statt des Punktes und dazu noch eckige Klammern statt der runden. Viele geben sich
mit einem der beiden Unterscheidungsmerkmale zufrieden:
.
Manche nennen das Vektorprodukt auch "äußeres Produkt". Wir wollen diesen Ausdruck für eine echte
innere Verknüpfung im Vektorraum jedoch verständlicherweise möglichst vermeiden.
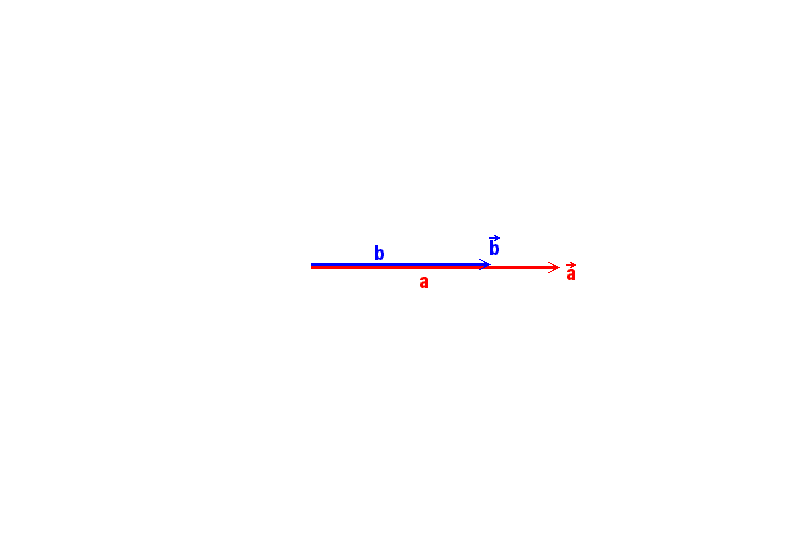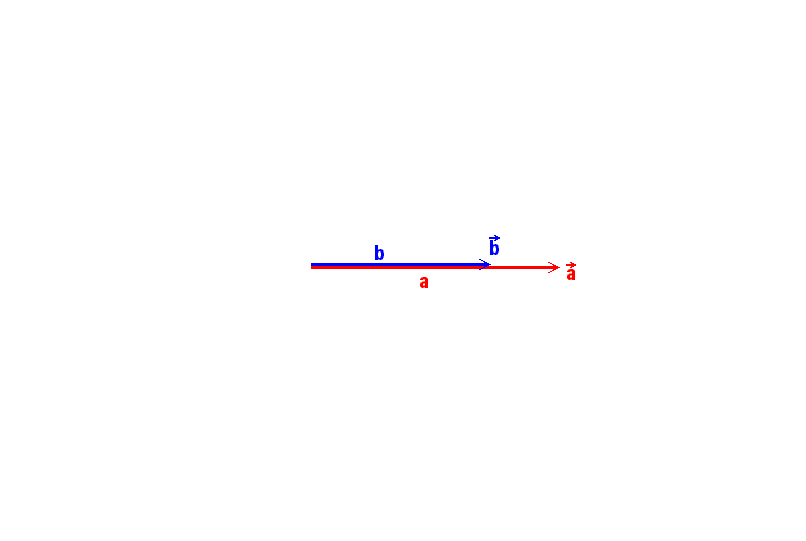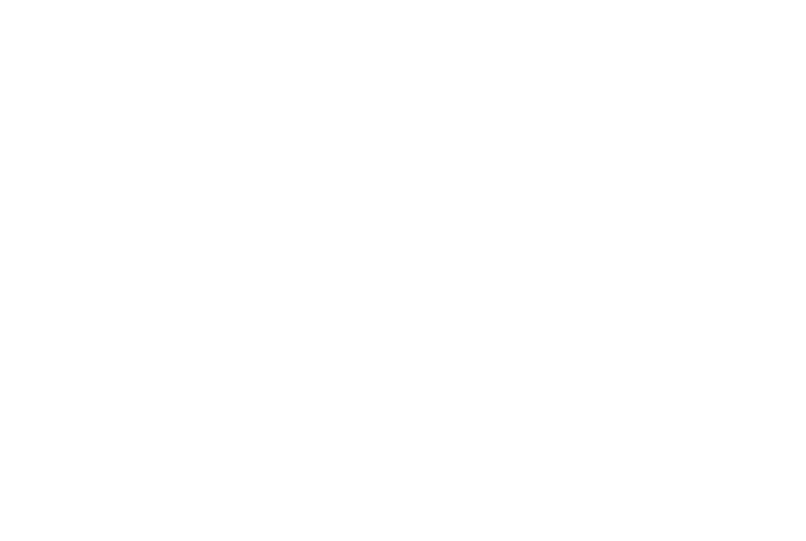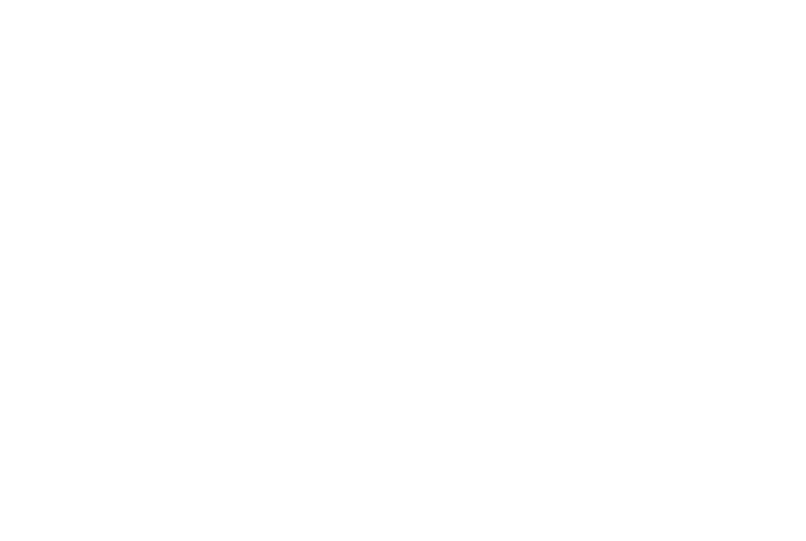
Wie beim Skalarprodukt betrachten wir zunächst wieder die Spezialfälle:
Für
und
kollinear, d.h. parallel oder antiparallel:
folgt
,
insbesondere:
Für
und
orthogonal, d.h.
senkrecht auf
:
folgt
,
insbesondere:
.
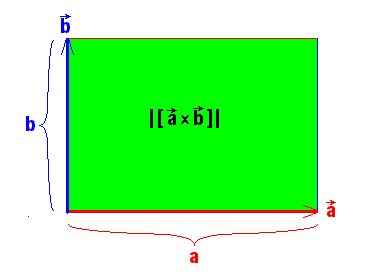
Die Länge des Produktvektors ist in diesem Fall maximal:
,
d.h. die Rechteckfläche mit den Längen der beiden Faktoren als Kantenlängen:
die Fläche des von den beiden Faktoren aufgespannten Parallelogramms oder von gleicher Größe: eine der
beiden im nächsten Bild farbig getönten Rechteckflächen mit den Höhen des Parallelogramms.
überschreitet,
wird der Sinus und folglich auch die Fläche negativ, was hier zu einer Umkehr der Richtung des Produktvektors
führt.
aus der Winkelgeschwindigkeit
und dem Ort
?
aus Ort
aus Ortsvektor
?
aus Kraft
und Hebelarm
?
in einem homogenen Magnetfeld
?
aus der Geschwindigkeit
und
Ladung 
und der magnetischen Induktion
?
des elektromagnetischen Strahlungsflusses aus dem elektrischen
und magnetischen Feld
nach dem Biot-Savartschen Gesetz? 
zwischen Dipolmoment
muss man an der angegebenen Stelle ziehen, damit das abgebildete starre T-Stück sich n i c h t um
den Drehpunkt