Distributivgesetz:
Wir nennen die Summe
 Einheitsvektor in Richtung von
Einheitsvektor in Richtung von
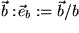 und betrachten die zur Richtung von
und betrachten die zur Richtung von
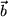 transversalen Anteile (siehe Abschnitt 9.5.1) der beiden Summanden
transversalen Anteile (siehe Abschnitt 9.5.1) der beiden Summanden
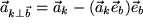 für
für
 und
wegen des Distributivgesetzes für das Skalarprodukt auch für
und
wegen des Distributivgesetzes für das Skalarprodukt auch für
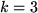 ,
die alle in der im folgenden Bild gezeigten Ebene senkrecht zu
,
die alle in der im folgenden Bild gezeigten Ebene senkrecht zu
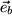 liegen:
liegen:
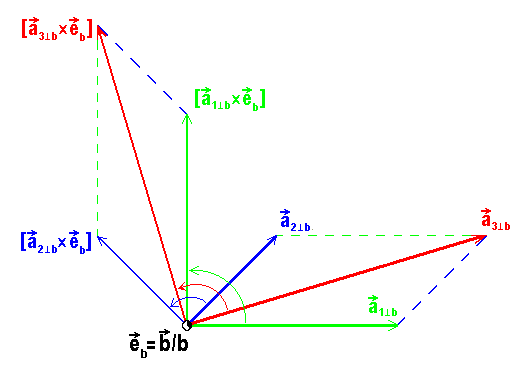
Bild 9.24: der Ebene senkrecht zu
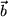 .
.
Die Produktvektoren
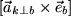 sind dann Vektoren der Länge
sind dann Vektoren der Länge
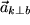 ,
die um
,
die um
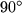 im Antiuhrzeigersinn gedreht, senkrecht auf den
im Antiuhrzeigersinn gedreht, senkrecht auf den
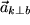 stehen. Das bedeutet aber, dass die ganze Vektoradditionsfigur um
stehen. Das bedeutet aber, dass die ganze Vektoradditionsfigur um
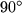 gedreht wurde, so dass immer noch gilt
gedreht wurde, so dass immer noch gilt
 .
Multiplikation dieser ganzen Gleichung mit
.
Multiplikation dieser ganzen Gleichung mit
 ergibt das behauptete Distributive Gesetz.
ergibt das behauptete Distributive Gesetz.
Zurück zum Text
 Einheitsvektor in Richtung von
Einheitsvektor in Richtung von
 und betrachten die zur Richtung von
und betrachten die zur Richtung von
 transversalen Anteile (siehe Abschnitt 9.5.1) der beiden Summanden
transversalen Anteile (siehe Abschnitt 9.5.1) der beiden Summanden
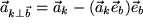 für
für
 und
wegen des Distributivgesetzes für das Skalarprodukt auch für
und
wegen des Distributivgesetzes für das Skalarprodukt auch für
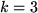 ,
die alle in der im folgenden Bild gezeigten Ebene senkrecht zu
,
die alle in der im folgenden Bild gezeigten Ebene senkrecht zu
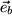 liegen:
liegen:
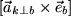 sind dann Vektoren der Länge
sind dann Vektoren der Länge
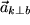 ,
die um
,
die um
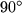 im Antiuhrzeigersinn gedreht, senkrecht auf den
im Antiuhrzeigersinn gedreht, senkrecht auf den
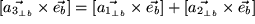 .
Multiplikation dieser ganzen Gleichung mit
.
Multiplikation dieser ganzen Gleichung mit
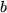 ergibt das behauptete Distributive Gesetz.
ergibt das behauptete Distributive Gesetz.