Um eine Komponentendarstellung für unser Vektorprodukt zu erhalten, müssen wir zunächst die Basisvektoren vektoriell multiplizieren. Wie oben schon angedeutet, bringt uns das Vektorprodukt die erwünschte einfache Darstellung der Tatsache, dass unsere Basisvektoren ein Rechtssystem bilden:
Rechtssystem: 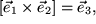 ,
,  ,
, 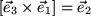
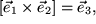 ,
,  ,
, 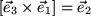
Wegen der Antikommutativität des Vektorprodukts kommen dazu noch drei weitere Relationen mit der umgekehrten Reihenfolge der Faktoren und einem Minuszeichen:
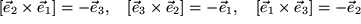
Analog wie beim Skalarprodukt durch das Kronecker-Symbol fassen wir diese sechs fundamentalen Relationen in eine einzige Gleichung zusammen durch die Einführung des nach Tullio Levi-Civita benannten Symbols: