Nun sind wir in der Lage zu berechnen, wie man das Vektorprodukt zweier Vektoren 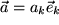 und
und 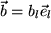 aus deren Komponenten erhält:
aus deren Komponenten erhält:
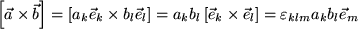
Wir erinnern noch einmal daran, dass die rechte Seite dieser Gleichung nach der Einsteinschen Konvention drei Summen über 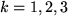 ,
, 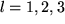 und
und 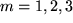 , also insgesamt 27 Summanden enthält, die wir aber natürlich nicht zu fürchten brauchen, weil wir wissen, dass 21 davon verschwinden und nur folgende sechs mit drei charakteristischen Minuszeichen übrigbleiben:
, also insgesamt 27 Summanden enthält, die wir aber natürlich nicht zu fürchten brauchen, weil wir wissen, dass 21 davon verschwinden und nur folgende sechs mit drei charakteristischen Minuszeichen übrigbleiben:
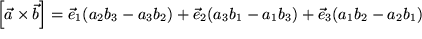
Hier sind die sechs Summanden jetzt nach Basisvektoren geordnet und zusammengefaßt, um leichter erkennen zu können, dass z.B: die 1-Komponente des Produktvektors sich folgendermaßen aus den Komponenten der beiden Faktoren ergibt: 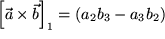 . Allgemein erhalten wir für die m-te Komponente:
. Allgemein erhalten wir für die m-te Komponente:
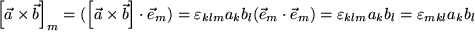 .
.
Die letzte Schreibweise ist wegen der zyklischen Vertauschbarkeit der Indizes beim Levi-Civita-Symbol gerechtfertigt.
Unsere Darstellung des Levi-Civita-Symbols als Determinante von Kronecker-Symbolen erlaubt noch weitere Schreibweisen für die Komponentendarstellung des Vektorprodukts, die leicht memorierbar und deshalb einigen von Ihnen möglicherweise schon begegnet sind:
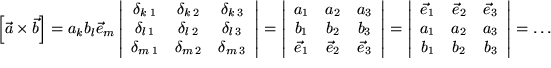
Um die letzte Form zu erhalten, wurden in der vorletzten Determinante die Zeilen zyklisch vertauscht. Auf diese Weise oder etwa durch Spiegelung der Determinante an ihrer Hauptdiagonalen lassen sich wieder eine ganze Reihe von Darstellungen finden, die alle gleichwertig sind, da sie zum selben Ergebnis führen. In der Praxis werden Sie natürlich auf etwa vorhandene Nullen achten und diejenige Form wählen, aus der Sie das gewünschte Resultat am schnellsten ersehen können.
Dabei ist die Determinantenschreibweise bei den letzten beiden Formen nur symbolisch gemeint und mit einiger Vorsicht zu genießen, denn, wie Sie sehen, stehen die Basisvektoren als Elemente in der Determinante, und das gibt es eigentlich nicht. Gemeint ist eine leicht einprägsame Merkformel für folgende häufig verwendete Entwicklung mit den Adjunkten:
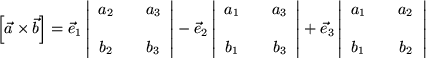
|
Aufgabe 9.38: Vektorprodukt als Determinante Berechnen Sie die Vektorprodukte von Aufgabe 9.36 als Determinanten. Lösung (1) (2) (3) |