Nachdem uns beide Produkte von zwei Vektoren zur Verfügung stehen, sind wir in der Lage, unser ursprüngliches Koordinatensystem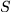 
mit dem Ursprung 
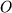auf elegante Weise zu charakterisieren: Unsere drei Basisvektoren 
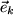mit 
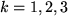bilden eine Orthonormale Rechtsbasis (:ONRB), d.h. sie:
| sind | 1) orthonormal: |  |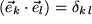
| bilden ein | 2) Rechtssystem: |  |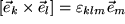
| und sind | 3) vollständig: |  |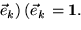
Neben diesem betrachten wir bei gleichbleibendem Ursprung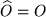 
noch ein anderes Koordinatensystem 
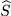, dessen Basisvektoren 
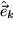mit 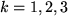durch eine lineare Transformation 
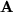aus den alten Basisvektoren hervorgehen:
Basistransformation: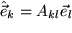 
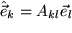
Die Elemente der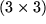 
-Transformationsmatrix 
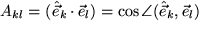erhalten wir durch skalare Multiplikation mit 
.
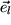Die Physiker interessiert nun folgende Frage:
Welche Matrizen sind zugelassen, wenn die neuen Basisvektoren wieder eine ONRB bilden sollen?