Statistical Physics and Condensed Matter
Anisotropic magnetic systems
Papers
(This work has been performed at the
School of Physics and Astronomy,
Raymond and Beverly Sackler Faculty of Exact Sciences, Tel Aviv University.)
J. Stein, O. Entin-Wohlman, A. Aharony:
Weak ferromagnetism in the low-temperature tetragonal phase of
the cuprates
Phys. Rev. B 53 (1996) 775
The criterion for the existence of weak ferromagnetism in the
low-temperature distorted phases of
La2CuO4-type compounds
is derived on the basis of a general superexchange Hamiltonian. It is
found that a ferromagnetic canting out of the CuO2 planes is
excluded in the pure low-temperature tetragonal phase. The anisotropic
superexchange interactions between the copper spins are obtained from a
Hubbard model which includes all copper 3d and oxygen 2p orbitals, and all
on-site Coulomb matrix elements. The results apply when the oxygen
octahedra surrounding each copper have tetragonal symmetry.
Explicit expressions
for the net ferromagnetic moment and the in-plane and the out-of-plane gaps
in the spin-wave spectrum are derived and estimated in terms of the
microscopic parameters of the cuprates.
J. Stein:
Nonlocal Coulomb interactions and the
magnetic anisotropies in the low-temperature phases of the cuprates
Phys. Rev. B 53 (1996) 785
We have extended and generalized earlier studies of the magnetic anisotropies
of the Cu spins
in the copper-oxide planes generated by the
spin-orbit coupling on the coppers and by the nonlocal
Coulomb interactions between neighboring ions.
Our derivation of the anisotropic magnetic
Hamiltonian includes the contributions from general matrix elements of
the Coulomb interaction both between the copper ions of a single bond
and between the adjacent copper and oxygen sites. The results apply
for a general rotation axis of the oxygen octahedra, with the assumption of
tetragonal site symmetry of the copper.
This mechanism leads to a
form of the anisotropic
spin interaction between the Cu ions which is identical to the
one generated by kinetic
superexchange in the presence of purely local Coulomb interactions.
Together with the numerical estimates for the resulting spin couplings,
this indicates that the Coulomb
direct exchange leads to significant
contributions to the isotropic spin interaction
and the out-of-plane anisotropy, but
does not affect qualitatively
the magnetic order in the ground state.
J. Stein:
Critical properties of a spin glass with anisotropic
Dzyaloshinskii-Moriya interaction
J. Phys. A 29 (1996) 963
We study the classical n-vector
spin glass with
anisotropic quenched random Dzyaloshinskii-Moriya (DM)
interaction. A random DM interaction with m
independent and separated couplings defines a
generalized gauge glass model with a
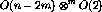 rotational symmetry and a broken global reflection invariance.
It is shown that this model is in the same universality
class as the random gauge XY ("gauge glass") model.
With an additional uniaxial anisotropy,
a crossover from Ising-like to gauge glass critical behaviour
is found for a
sufficiently large variance of the
DM interaction.
A new situation arises when there is correlation between
the separated random DM couplings.
We show that the critical behaviour of a spin glass
with two correlated couplings of the anisotropic DM interaction
is in a new universality
class. The critical exponents eta and nu of this model are calculated
at two-loop order near six dimensions.
We also present a simplified and more rigorous field theoretic analysis
of the gauge glass
model.
rotational symmetry and a broken global reflection invariance.
It is shown that this model is in the same universality
class as the random gauge XY ("gauge glass") model.
With an additional uniaxial anisotropy,
a crossover from Ising-like to gauge glass critical behaviour
is found for a
sufficiently large variance of the
DM interaction.
A new situation arises when there is correlation between
the separated random DM couplings.
We show that the critical behaviour of a spin glass
with two correlated couplings of the anisotropic DM interaction
is in a new universality
class. The critical exponents eta and nu of this model are calculated
at two-loop order near six dimensions.
We also present a simplified and more rigorous field theoretic analysis
of the gauge glass
model.
J. Stein:
Critical exponents of the 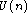 vector
spin glasses
vector
spin glasses
Europhys. Lett. 34 (1996) 717
The critical exponents of the classical spin glasses with
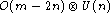 symmetry are obtained to order
symmetry are obtained to order
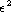 of
the
of
the  -expansion around six dimensions,
where
-expansion around six dimensions,
where 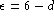 .
This new unitary symmetry is realized in the
m-vector (
.
This new unitary symmetry is realized in the
m-vector (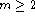 ) spin glasses with
anisotropic quenched random Dzyaloshinskii-Moriya (DM) interaction.
Such a random DM interaction with n correlated couplings leads to
critical exponents which are different from those of any isotropic
m-vector spin glass and thus belong to new universality classes.
) spin glasses with
anisotropic quenched random Dzyaloshinskii-Moriya (DM) interaction.
Such a random DM interaction with n correlated couplings leads to
critical exponents which are different from those of any isotropic
m-vector spin glass and thus belong to new universality classes.
Statistical Physics Group,
Jürgen Stein
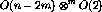 rotational symmetry and a broken global reflection invariance.
It is shown that this model is in the same universality
class as the random gauge XY ("gauge glass") model.
With an additional uniaxial anisotropy,
a crossover from Ising-like to gauge glass critical behaviour
is found for a
sufficiently large variance of the
DM interaction.
A new situation arises when there is correlation between
the separated random DM couplings.
We show that the critical behaviour of a spin glass
with two correlated couplings of the anisotropic DM interaction
is in a new universality
class. The critical exponents eta and nu of this model are calculated
at two-loop order near six dimensions.
We also present a simplified and more rigorous field theoretic analysis
of the gauge glass
model.
rotational symmetry and a broken global reflection invariance.
It is shown that this model is in the same universality
class as the random gauge XY ("gauge glass") model.
With an additional uniaxial anisotropy,
a crossover from Ising-like to gauge glass critical behaviour
is found for a
sufficiently large variance of the
DM interaction.
A new situation arises when there is correlation between
the separated random DM couplings.
We show that the critical behaviour of a spin glass
with two correlated couplings of the anisotropic DM interaction
is in a new universality
class. The critical exponents eta and nu of this model are calculated
at two-loop order near six dimensions.
We also present a simplified and more rigorous field theoretic analysis
of the gauge glass
model.
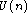 vector
spin glasses
vector
spin glasses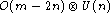 symmetry are obtained to order
symmetry are obtained to order
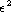 of
the
of
the  -expansion around six dimensions,
where
-expansion around six dimensions,
where 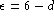 .
This new unitary symmetry is realized in the
m-vector (
.
This new unitary symmetry is realized in the
m-vector (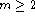 ) spin glasses with
anisotropic quenched random Dzyaloshinskii-Moriya (DM) interaction.
Such a random DM interaction with n correlated couplings leads to
critical exponents which are different from those of any isotropic
m-vector spin glass and thus belong to new universality classes.
) spin glasses with
anisotropic quenched random Dzyaloshinskii-Moriya (DM) interaction.
Such a random DM interaction with n correlated couplings leads to
critical exponents which are different from those of any isotropic
m-vector spin glass and thus belong to new universality classes.