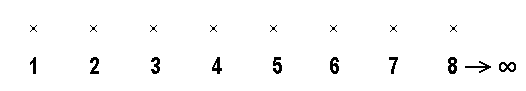Wir beginnen mit der Menge der natürlichen Zahlen
, von den Zahlentheoretikern mit
bezeichnet und "natürlich" genannt, weil sie von den Menschen, soweit die Erinnerung reicht, zum Zählen benutzt wurden. Die Physiker denken dabei etwa an Teilchenzahlen, z.B. die Zahl
der Atome oder Moleküle in einem Mol.
Seit alters gibt es für die natürlichen Zahlen zwei verschiedene Verknüpfungen: die Addition und die Multiplikation, die je zwei natürlichen Zahlen
( "die Zahlen
und
sind Elemente aus der Menge
" ) eine neue natürliche Zahl zuordnen, weshalb sie interne Verknüpfungen genannt werden:
| die ADDITION: | ||||
| interne Verknüpfung: |
 |
mit dem | ||
| Kommutativen Gesetz: |
 |
und dem | ||
| Assoziativen Gesetz: |
 |
und | ||
| die MULTIPLIKATION: | ||||
| interne Verknüpfung: |
 oder
 |
ebenfalls mit einem | ||
| Kommutativen Gesetz: |
 |
und einem | ||
| Assoziativen Gesetz: |
 |
und darüber hinaus einem | ||
| Neutralem Element: der Eins: |
 |
die beiden Verknüpfungsoperationen, Addition und Multiplikation, sind durch das
| Distributive Gesetz: |  |
miteinander verbunden. |
Anschaulich kann man sich die natürlichen Zahlen als äquidistante Punkte auf einer Halbgeraden vorstellen:
hinzuzunehmen, also
zu ergänzen. Dadurch erhält auch die Addition ein eindeutig bestimmtes
