Die letzte wichtige Eigenschaft der Funktionen, die wir brauchen, ist die Stetigkeit: Insbesondere in der klassischen Physik stellen wir uns häufig mit Erfolg auf den Standpunkt: "Natura non facit saltus" (Die Natur macht keine Sprünge), d.h. wir betrachten stetige Funktionen. Für viele Experimente ist die Stetigkeit schon wegen der endlichen Meßgenauigkeit als Hypothese unentbehrlich. Aber natürlich gibt es auch unstetige Prozesse, z.B. beim Ein- oder Ausschalten und bei "Quantensprüngen".
Die Mathematiker definieren eine Funktion als stetig an einer Stelle  , wenn sie dem Punkt
, wenn sie dem Punkt  benachbarte Punkte wieder in benachbarte Bildpunkte abbildet, in Kurzschrift:
benachbarte Punkte wieder in benachbarte Bildpunkte abbildet, in Kurzschrift:
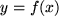 stetig bei
stetig bei 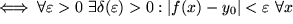 mit
mit 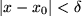
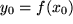 des Grenzwerts
des Grenzwerts 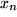 aus dem Definitionsbereich der Argumente gegeben werden:
aus dem Definitionsbereich der Argumente gegeben werden: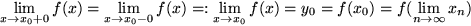
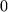 um
um 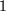 :
: 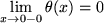 während doch
während doch 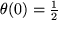 war. Die Normalhyperbel
war. Die Normalhyperbel 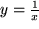 ist zwar an der Stelle
ist zwar an der Stelle  unstetig, aber dort auch nicht definiert.
unstetig, aber dort auch nicht definiert.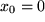
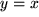
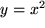
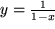
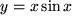
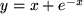
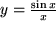
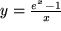
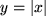
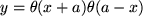
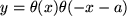

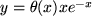
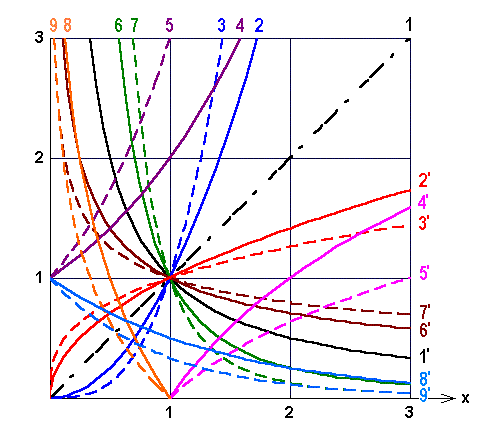
 (z.B. der elektrischen Spannung) durch deren Variation zwischen den Werten 0 und 3 mehrfach genau gemessen und Ihre Messwerte werden durch eine der 18 im Bild 4.28 skizzierten Kurven innerhalb Ihrer Messgenauigkeit gut beschrieben. Welche einfachen Hypothesen über die funktionale Abhängigkeit der gemessenen Größe
(z.B. der elektrischen Spannung) durch deren Variation zwischen den Werten 0 und 3 mehrfach genau gemessen und Ihre Messwerte werden durch eine der 18 im Bild 4.28 skizzierten Kurven innerhalb Ihrer Messgenauigkeit gut beschrieben. Welche einfachen Hypothesen über die funktionale Abhängigkeit der gemessenen Größe