4 Funktionen

4.2 Funktionen - Grundausstattung

4.2.3 Exponentialfunktionen

Beim Potenzieren haben wir zunächst nur natürliche Zahlen als Exponenten eingeführt, die angeben, wie oft eine reelle Basiszahl als Faktor vorkommt:

und die Rechenregeln

erhalten.

Dann haben wir negative Exponenten durch die Definition hinzugenommen und durch die Konvention die Zahlenmenge der Exponenten auf die ganzen Zahlen erweitert.

Zur Klasse der Exponentialfunktionen kommt man, indem man statt der ganzen Zahlen ( wie bei den Basiszahlen ) reelle Zahlen als Exponenten zuläßt: mit und sich auf positive Basiszahlen beschränkt, ohne dabei die Rechenregeln für die Potenzen zu ändern, d.h. mit folgenden

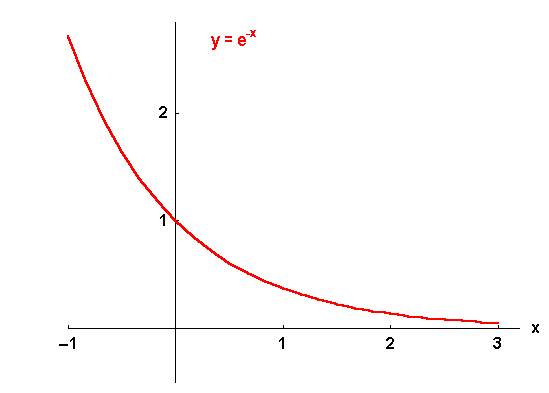
Von zentraler Wichtigkeit für alle Naturwissenschaften ist dabei die natürliche Exponentialfunktion mit der in Abschnitt 3.5: definierten irrationalen Zahl als Basis

deren Graph mit seinem charakteristischen rasanten Anwachsen in folgendem Bild direkt gemessen werden kann:

Bild 4.8: Aufbau der Exponentialfunktion z.B. beim Anwachsen der Zahl der Zellen mit einer festen Teilungsrate.

Für die Physiker ist auch die inverse Funktion von großer Bedeutung für alle Dämpfungs- und Zerfallsprozesse. Auch sie ist der Messung direkt zugänglich, z.B. beim radioaktiven Zerfall, bei dem die jeweils noch vorhandene Menge den Zerfall bestimmt: , wobei die Zahl der Kerne zur Zeit ist und die Abklingzeit:

Bild 4.9: Inverse Exponentialfunktion, z.B. beim radioaktiven Zerfall

Auch für die Exponentialfunktionen werden wir im Kapitel 6 eine Methode kennenlernen, die es uns ermöglicht, den Funktionswert zu jedem Wert der Variablen durch elementare Rechenoperationen wie Addition und Multiplikation bis zu jeder gewünschten Genauigkeit auszurechnen.

Folgende Kombinationen der beiden natürlichen Exponentialfunktionen haben ihrer Wichtigkeit wegen besondere Namen erhalten, die wir erst später richtig verstehen werden: Der

auch Kettenlinie genannt, weil eine Kette im Schwerefeld der Erde nach diesem Funktionsverlauf zwischen ihren Aufhängepunkten durchhängt, und der

mit der leicht verifizierbaren Relation

Dazu kommt analog den trigonometrischen Funktionen noch der Quotient der beiden, der

und der

Das folgende Bild zeigt die Graphen dieser Funktionen, die unter der Bezeichnung hyperbolische Funktionen zusammengefaßt werden.

Bild 4.10: Hyperbolische Funktionen