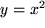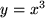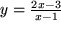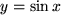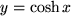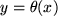4 Funktionen

4.7 Eineindeutigkeit

Wie wir bei der Einführung des Funktionsbegriffs besonders erwähnt hatten, enthält die Definition zwar die Eindeutigkeit der Abbildung, d.h. zu jedem Urbildpunkt existiert genau ein Bildpunkt 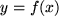, aber es ist immer noch möglich, dass zwei verschiedene Argumente denselben Funktionswert als Bildpunkt haben, d.h. 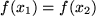für 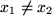. Funktionen, bei denen das nicht mehr vorkommen kann, haben einen besonderen Namen: Man nennt eine Funktion eineindeutig ( auch umkehrbar eindeutig oder bijektiv ) in einem Intervall 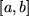, wenn auch jeder Funktionswert 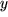aus dem entsprechenden Wertevorrat nur bei genau einem Argument auftritt:

Bild 4.18: Graph einer Geraden und der Normalparabel

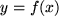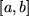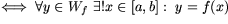
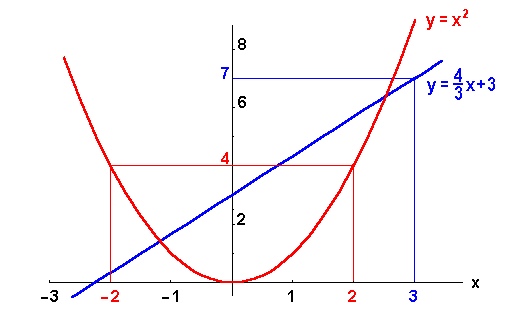
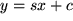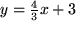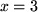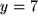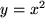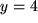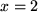Das Bild zeigt als Beispiel für eine eineindeutige Funktion eine Gerade , speziell , bei der z.B. dem Variablenwert genau der Funktionswert entspricht, und als Gegenbeispiel die Normalparabel , bei der man den Funktionswert aus und 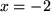erhält.