Als Umkehrfunktion der natürlichen Exponentialfunktion
erhalten wir durch Spiegelung des Graphen an der Winkelhalbierenden für
den nur ganz langsam ansteigenden natürlichen Logarithmus
:
Als Umkehrfunktion der natürlichen Exponentialfunktion
erhalten wir durch Spiegelung des Graphen an der Winkelhalbierenden für
den nur ganz langsam ansteigenden natürlichen Logarithmus
:
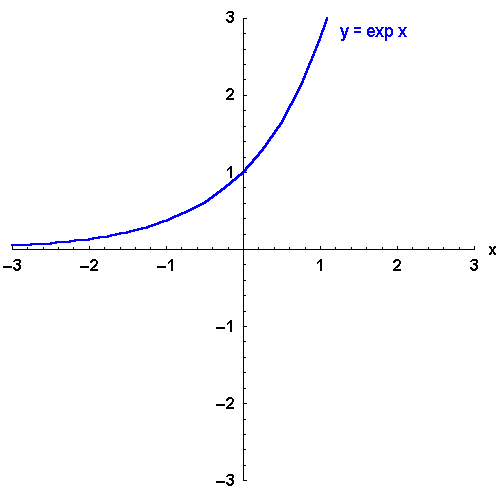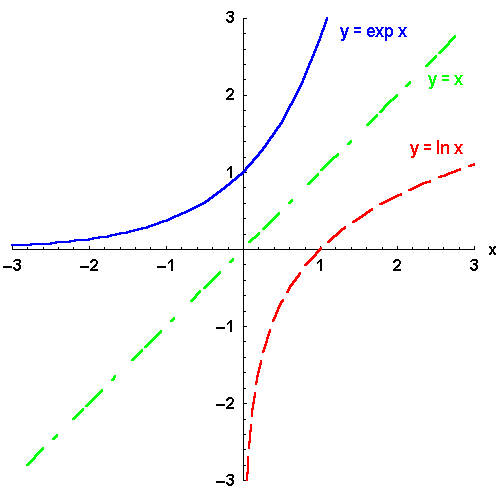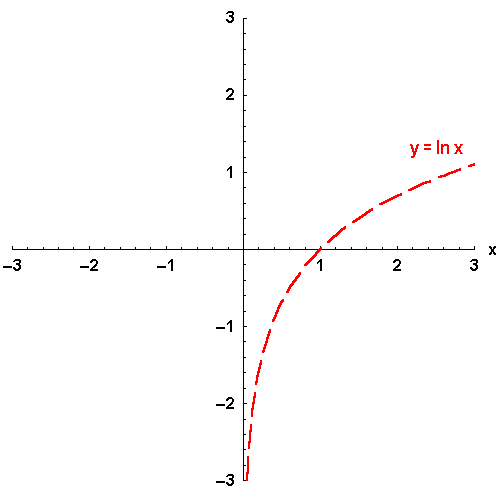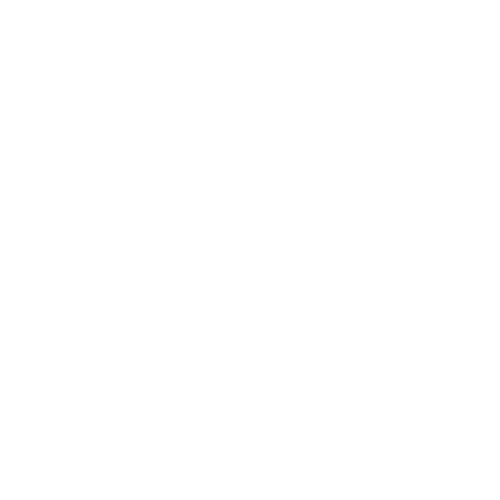
Bild 4.22: Exponenialfunktion und ihre Umkehrfunktion, der natürliche Logarithmus
Die Eigenschaften des streng monoton ansteigenden natürlichen Logarithmus sind an dem abgebildeten Graphen abzulesen:
und
. Aus den Rechenregeln der Potenzen erhalten wir folgende Rechenregeln für die natürlichen Logarithmen:
,
und
.
Nachdem wir speziell mit der natürlichen Exponentialfunktion und dem natürlichen Logarithmus vertraut sind, können sie dazu dienen, die allgemeine Exponentialfunktion zu definieren:
für
und als deren Umkehrfunktion den allgemeinen Logarithmus
,
der für
(wie auch
) streng monoton ansteigt, für
jedoch monoton fällt.
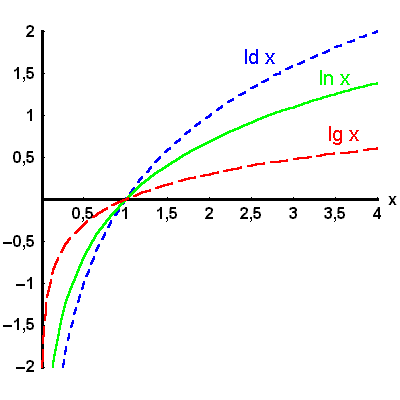
Bild 4.23: Die drei wichtigsten Logarithmen zu den Basen: 2,
, und 10
Als Rechenregeln für die allgemeinen Logarithmen erhalten wir bei gleichbleibender Basis
:
,
und
.
Neben den besonders wichtigen natürlichen Logarithmen
mit der nichtrationalen Zahl
als Basis gibt es noch für zwei weitere häufig gebrauchte Basen einfachere Schreibweisen: die dualen
(oder englisch: binary logarithms
)
und die dekadischen oder Briggschen Logarithmen
.
Die Umrechnung zwischen Logarithmen verschiedener Basen erfolgt nach der Formel:
speziell z.B. für
und
:
,
denn durch dreimalige Anwendung der Identität
erhalten wir
und folglich sind die Exponenten gleich.
|
Aufgabe 4.12: Logarithmen a) Was ist
b) Zeigen Sie, dass
c) Berechnen Sie
d) Berechnen Sie
|
Auch die allgemeine Potenzfunktion wird mit Hilfe der natürlichen Exponentialfunktion und des natürlichen Logarithmus für
und
definiert durch:
für
und
,
von uns jedoch wenig gebraucht werden:
Bild 4.24: Potenzfunktionen
Wichtiger sind für die Physik die Umkehrfunktionen der Hyperbel-Funktionen:
,
und
, die wir aus natürlichen Exponentialfunktionen aufgebaut hatten: Sie heißen Area - Funktionen, können selbstverständlich durch natürliche Logarithmen ausgedrückt werden und sind aus dem nächsten Bild zu entnehmen:
zu  |
 , |
|
zu  |
 , |
|
zu  |
 . |
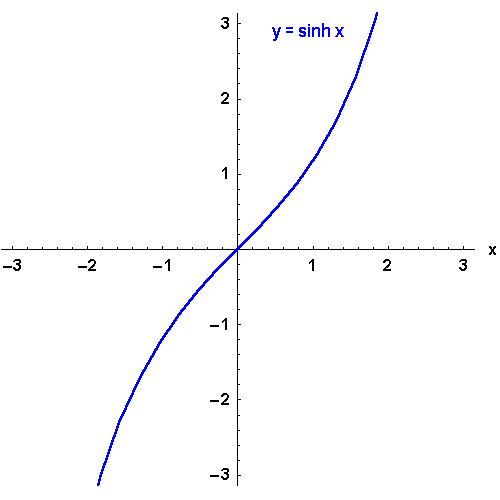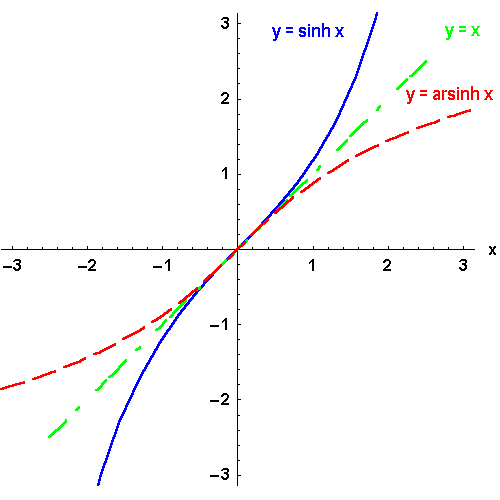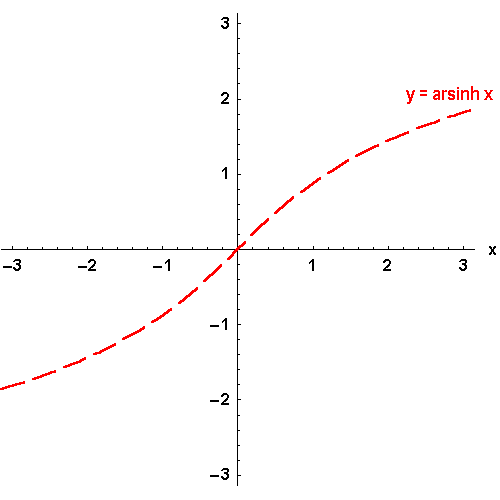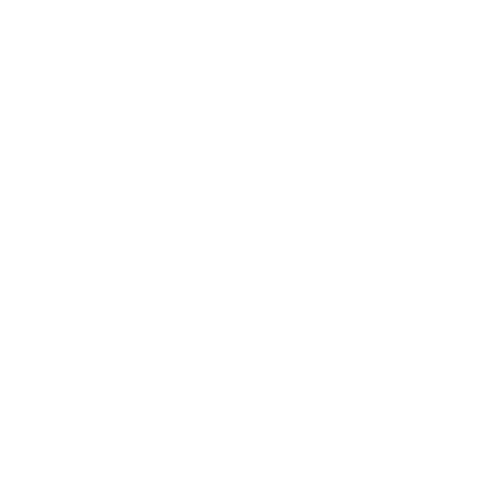
Bild 4.25a: Der Sinus hyperbolicus und seine Umkehrfunktion: y = arsinh x
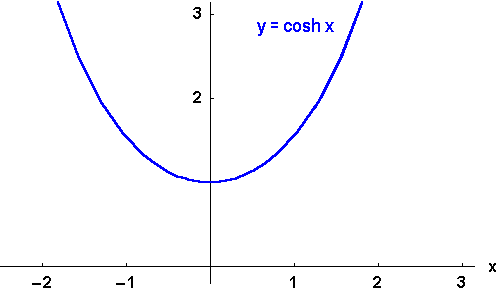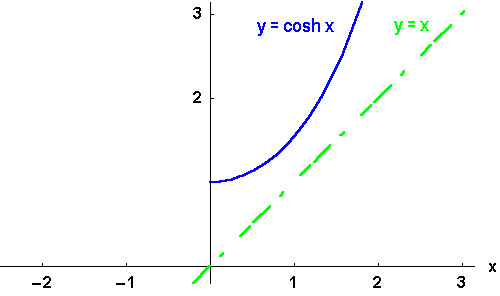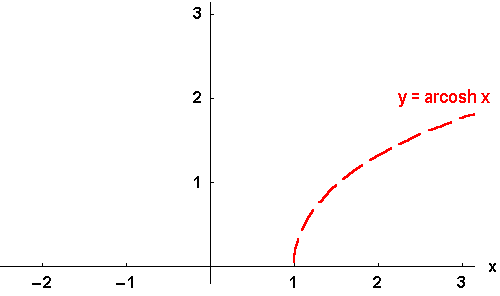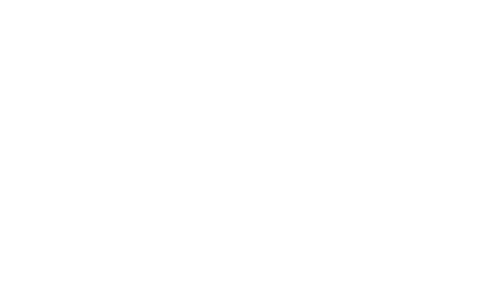
Bild 4.25b: Der Cosinus hyperbolicus und seine Umkehrfunktionen: y = arcosh x
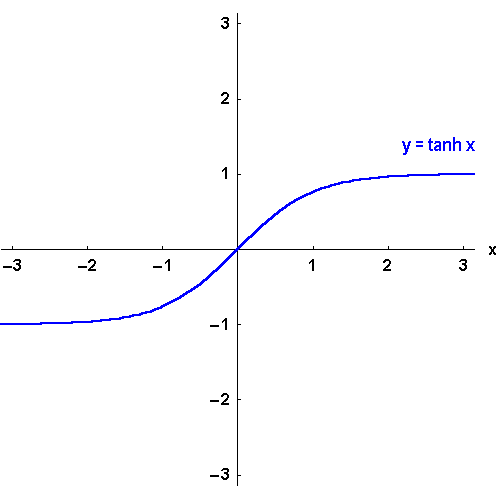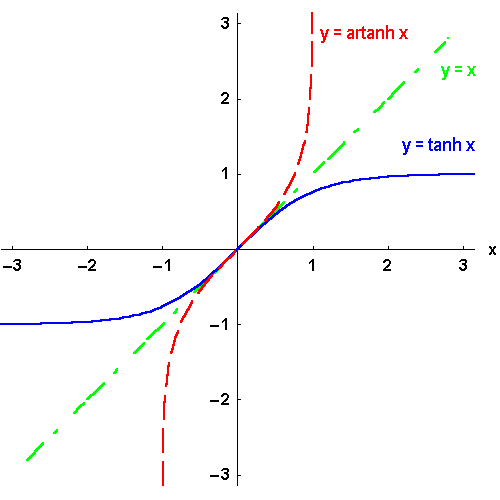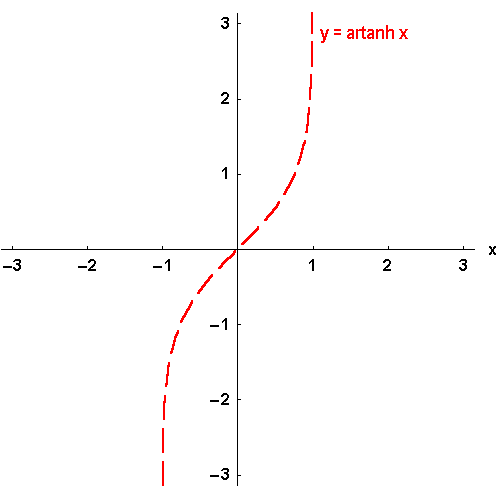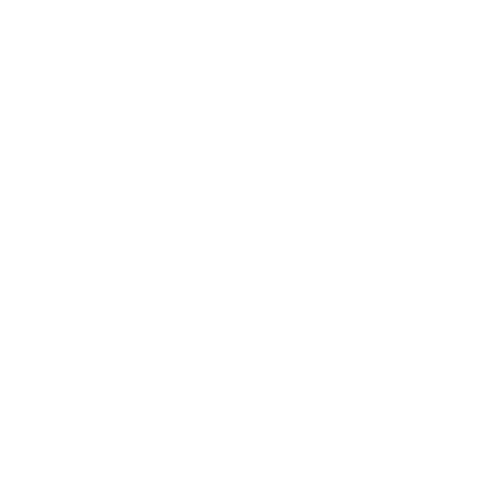
Bild 4.25c: Der Tangens hyperbolicus und seine Umkehrfunktionen: y = artanh x
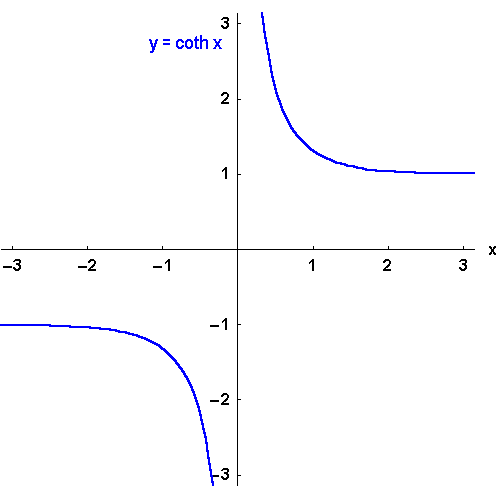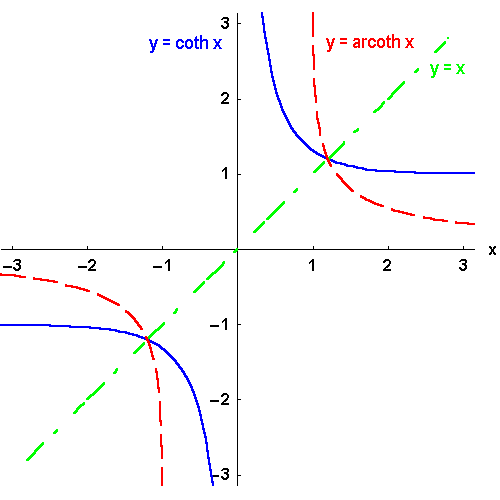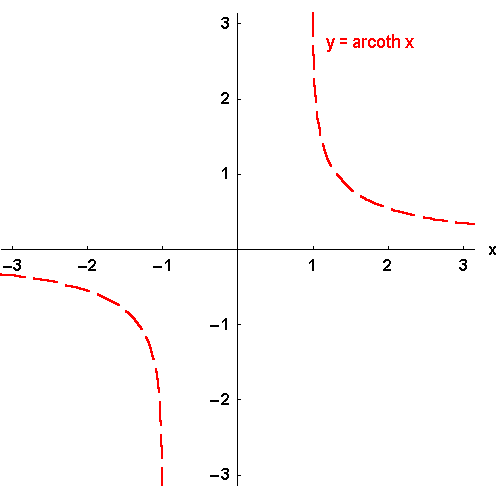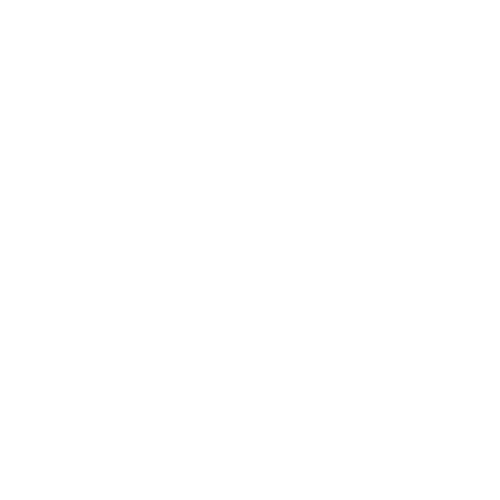
Bild 4.25d: Der Cotangens hyperbolicus und seine Umkehrfunktionen: y = arcoth x
? 
bzw.
. 
aus
. 
. 
folgt
. 
folgt
.