Um die in der Physik auftretenden Funktionen zu differenzieren, brauchen wir, wie man schon aus den Blanks in der TABELLE sieht, zu diesen einfachen meist aus der Schule bekannten Regeln zwei weitere Differentiationsregeln:
Bei der Differentiation verketteter Funktionen hilft uns die Kettenregel: Sie gibt uns den Differentialquotienten einer mittelbaren Funktion ![]() aus den Differentialquotienten der eingesetzten "inneren" Funktion
aus den Differentialquotienten der eingesetzten "inneren" Funktion ![]() und der "äußeren" Funktion
und der "äußeren" Funktion ![]() , in die eingesetzt wurde mit
, in die eingesetzt wurde mit ![]() . Mit den Bezeichnungen von Leibniz erhalten wir das Produkt aus der sogenannten "äußeren"
. Mit den Bezeichnungen von Leibniz erhalten wir das Produkt aus der sogenannten "äußeren" ![]() und der "inneren" Ableitung
und der "inneren" Ableitung ![]() :
:
in Leibniz-Schreibweise oder in Lagrange-Schreibweise:
Nachdem wir mit dem Begriff der Differentiale vertraut sind, erscheint uns dieses Resultat als Trivialität, da einfach mit ![]() erweitert wurde. Dennoch wollen wir den Beweis kurz skizzieren zur Demonstration der Vorteile der Differentiale, mit deren Hilfe er nämlich besonders einfach wird:
erweitert wurde. Dennoch wollen wir den Beweis kurz skizzieren zur Demonstration der Vorteile der Differentiale, mit deren Hilfe er nämlich besonders einfach wird:
Zuerst für die "innere" Funktion ![]() mit
mit ![]() ,
,
dann für die "äußere" Funktion ![]() mit
mit ![]() ,
,
nach Einsetzen ergibt dies: ![]() , was nach Division durch das Differential
, was nach Division durch das Differential ![]() im Grenzwert übergeht in:
im Grenzwert übergeht in:
Folgendes Beispiel illustriert die Vorteile der Leibnizschen Schreibweise:
Gesucht werde die erste Ableitung von ![]() für
für ![]() :
:
denn ![]() mit
mit ![]() ,
, ![]() mit
mit ![]() und
und ![]() mit
mit ![]() .
.
Ein weiteres Beispiel ist die
Beweis mit ![]() :
: ![]()
![]() .
.
|
Aufgaben 5.3: Kettenregel Berechnen Sie folgende Differentialquotienten nach der Kettenregel:
|
Schließlich brauchen wir noch die Umkehrfunktions-Regel für den Differentialquotienten der Umkehrfunktion ![]() mit
mit ![]() einer differenzierbaren eineindeutigen Funktion
einer differenzierbaren eineindeutigen Funktion ![]() mit
mit ![]() , deren Differentialquotient
, deren Differentialquotient ![]() bekannt ist und im ganzen
bekannt ist und im ganzen ![]() nicht verschwindet:
nicht verschwindet:
Wir wollen nur diese in der Leibnizschen Schreibweise suggestiv einfache und vom Standpunkt der Differentiale triviale Formel herleiten: Dazu bilden wir die Ableitung von ![]() nach
nach ![]() nach der Kettenregel:
nach der Kettenregel:
Mit diesem Vorrat an Regeln können wir nun alle gewünschten Ableitungen berechnen. Die meisten Beweise finden Sie in Schubladen:
Zunächst die
als Umkehrfunktion von ![]() für
für ![]() , denn
, denn ![]() , d.h. unsere Potenzregel (*) gilt auch für reziproke Exponenten.
, d.h. unsere Potenzregel (*) gilt auch für reziproke Exponenten.
Dann allgemein für eine
D.h. die Potenzregel (*) gilt auch für beliebige rationale Exponenten.
Dann den
als Umkehrfunktion der Exponentialfunktion ![]() für
für ![]() .
.
Es gilt sogar: ![]() . Denn
. Denn ![]() für
für ![]() .
.
Dann betrachten wir die
D.h. unsere Potenzregel (*) gilt universell auch für beliebige reelle Exponenten.
Auch für den
zu einer beliebigen reellen Basis ![]() erhalten wir jetzt die Ableitung, und zwar als Umkehrfunktion der allgemeinen Exponentialfunktion
erhalten wir jetzt die Ableitung, und zwar als Umkehrfunktion der allgemeinen Exponentialfunktion ![]() :
:
Wir schließen diese auch für das übernächste Kapitel noch wichtige Liste der Differentialquotienten mit den zyklometrischen Funktionen und den Area-Funktionen ab:
Für den
Analog für den
|
Aufgabe 5.4: Beweisen Sie das mit der Umkehrfunktion: |
Für den
Analog für
|
Aufgabe 5.5: Beweisen Sie das mit der Umkehrfunktion: |
Die Area-Funktionen, die Umkehrfunktionen der Hyperbel-Funktionen, vervollständigen unsere Differentiationstabelle:
Für den
und den
|
Aufgabe 5.6: Beweisen Sie das mit der Umkehrfunktion: |
Für den
und
|
Aufgabe 5.7: Beweisen Sie das mit der Umkehrfunktion: |
Alle gewonnenen Ergebnisse finden Sie in der großen Differentiationtabelle vereint, auf die wir später noch oft zurückkommen werden:
| TABELLE ZUR DIFFERENTIATION | |||
| Zeile | Bemerkungen: | ||
| 1 | 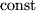 |
||
| 2 | 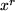 |
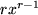 |
|
| 3 | |||
| 4 | |||
| 5 | 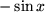 |
||
| 6 | 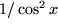 |
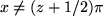 , ,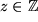 |
|
| 7 | 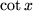 |
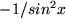 |
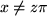 , ,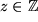 |
| 8 |  |
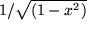 |
|
| 9 | 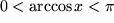 |
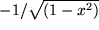 |
|
| 10 | 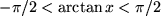 |
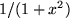 |
|
| 11 |  |
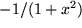 |
|
| 12 | |||
| 13 | 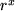 |
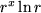 |
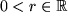 |
| 14 | 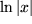 |
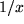 |
|
| 15 | 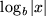 |
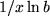 |
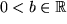 , ,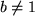 |
| 16 | 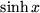 |
||
| 17 | 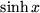 |
||
| 18 | 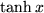 |
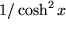 |
|
| 19 | 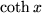 |
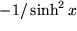 |
|
| 20 | 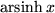 |
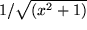 |
|
| 21 | 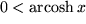 |
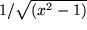 |
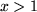 |
| 22 | 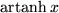 |
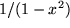 |
|
| 23 | 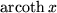 |
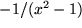 |
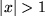 |
|
Aufgabe 5.8: Differentiationsbeispiele Bestimmen Sie die Differentialquotienten für folgende Funktionen
Berechnen Sie die ersten fünf Ableitungen folgender Funktionen
|