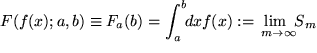7 Integration

7.2 Fläche unter einer Funktion über einem Intervall

Den gesuchten Flächeninhalt 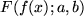"unter" einer beliebigen beschränkten stetigen, aber zunächst positiven Funktion 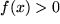"über" der endlichen Wegstrecke "zwischen" Anfangspunkt und Endpunkt 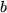, oft auch einfach 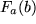genannt, erhalten wir nach dem oben für eine Gerade angedeuteten Rezept: Wir teilen die zu berechnende Fläche in viele schmale senkrechte Streifen, deren obere Seiten annähernd gerade sind, berechnen die Flächeninhalte der Streifen wie oben, summieren die einzelnen Anteile auf und lassen schließlich die Zahl der Streifen über alle Grenzen wachsen in der Hoffnung, so den gesuchten Flächeninhalt als Grenzwert zu finden.

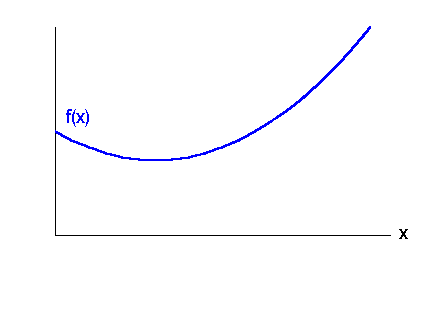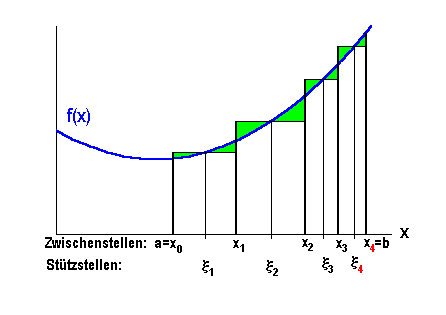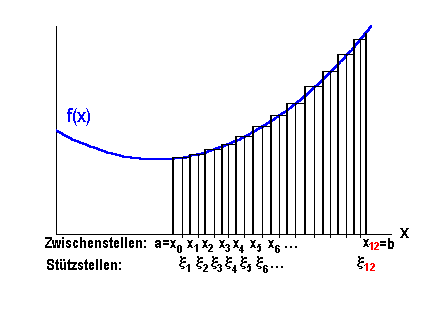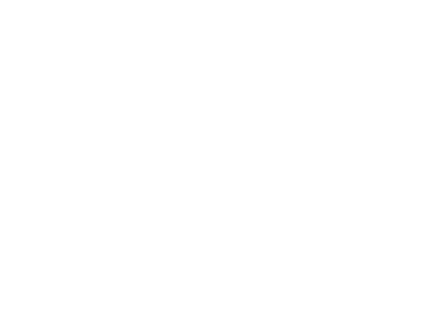
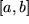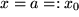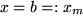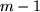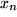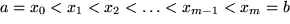Wir wollen diesen Grenzprozeß ein einziges Mal im einzelnen schildern und dann standardisiert ablaufen lassen: Das Intervall zwischen dem Anfangspunkt, genannt, und dem Endpunkt, genannt, wird durch die Wahl von z.B. Zwischenstellen mit in 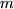Teilintervalle 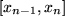der jeweiligen Länge 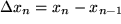geteilt. Die Teilintervalle brauchen keineswegs, können aber sehr wohl alle gleich lang sein: 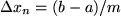. Im Inneren jedes der kleinen Teilintervalle wählen wir eine Stützstelle 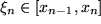, die nicht unbedingt auch der arithmetische Mittelpunkt 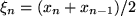zu sein braucht, aber ohne weiteres sein kann. Dann bestimmen wir die Funktionswerte über diesen Stützstellen und nähern den wirklichen Flächeninhalt der einzelnen Streifen durch 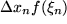, den der entsprechenden Rechtecke unter den Horizontalen durch die 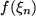. Diese 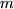Rechteckflächen summieren wir auf und nennen sie

Bild 7.3: Intervallteilung und Streifen

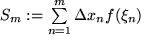
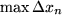Der angekündigte Grenzübergang besteht nun aus der Verfeinerung der Intervallzerlegung, indem wir die Anzahl der Zwischenstellen über alle Grenzen anwachsen lassen, wobei wir bei nichtäquidistanter Teilung darauf achten müssen, dass die Breite des dicksten Streifens gegen Null strebt. Falls die Folge der Riemann-Summen 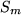dann einen Grenzwert besitzt, der unabhängig ist von der Zerlegung des Intervalls und von der Auswahl der Stützstellen 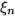in den einzelnen Streifen, dann nennen wir diesen Grenzwert das "bestimmte" (oder Riemann-) Integral der Funktion von nach , bzw. 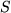den Flächeninhalt "unter" der Funktion "über" dem Intervall und schreiben nach den Vorschlägen von Leibniz mit einem stilisierten für Summe:

Der Integrand kann auch zwischen das Integralzeichen und das Differential gepackt werden.

Die Mathematiker garantieren uns, dass der betrachtete Grenzwert existiert, falls die zu integrierende Funktion stetig und beschränkt sowie das Intervall endlich und abgeschlossen ist:

Die Differenzierbarkeit folgte ja im Gegensatz dazu keineswegs aus der Stetigkeit.