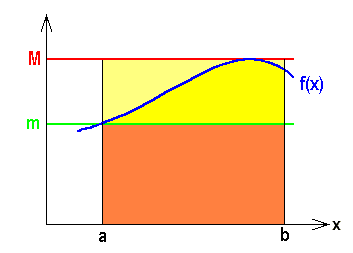
Auch einige Ungleichungen erweitern unser Verständnis für den Integralbegriff und sind später hilfreich beim Berechnen von Integralen:
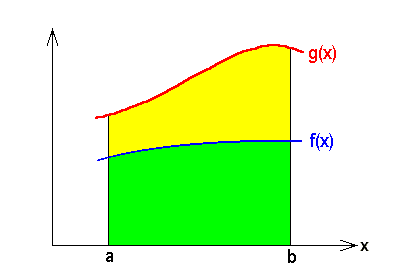
Falls z.B. eine Funktion ![]() in einem ganzen Intervall
in einem ganzen Intervall ![]() größer ist als eine andere Funktion
größer ist als eine andere Funktion ![]() , folgt für die entsprechende Relation für die Integrale die sogenannte
, folgt für die entsprechende Relation für die Integrale die sogenannte
 ,
,
weil eine analoge Relation für Summen gilt.
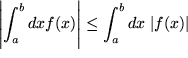 für
für 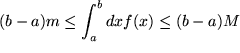 , falls
, falls