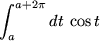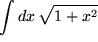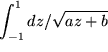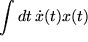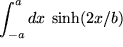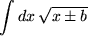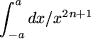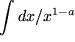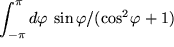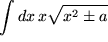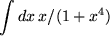Die Substitution ist immer dann anzuraten, wenn der Integrand  stetig von einer anderen Variablen
stetig von einer anderen Variablen 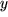 einfacher oder zweckmäßiger abhängt, die mit
einfacher oder zweckmäßiger abhängt, die mit 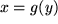 umkehrbar eindeutig und stetig differenzierbar zusammenhängt, wobei
umkehrbar eindeutig und stetig differenzierbar zusammenhängt, wobei 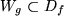 .
.
Der Klarheit wegen nennen wir die Integrationsgrenzen des gesuchten Integrals 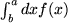 jetzt
jetzt 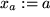 bzw.
bzw. 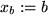 : also
: also 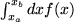 . Wegen der umkehrbar eindeutigen Zuordnung von
. Wegen der umkehrbar eindeutigen Zuordnung von 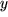 und
und  gibt es eine Umkehrfunktion
gibt es eine Umkehrfunktion 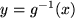 , insbesondere sind
, insbesondere sind  und
und 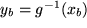 , und außerdem existiert wegen der stetigen Differenzierbarkeit die Ableitung:
, und außerdem existiert wegen der stetigen Differenzierbarkeit die Ableitung: 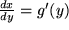 . Dann gilt (in der suggestiven Schreibweise von Leibniz fast trivialerweise) die:
. Dann gilt (in der suggestiven Schreibweise von Leibniz fast trivialerweise) die:
|
Substitutionsformel |
Erfahrungsgemäß ist die Erklärung des Substitutionsverfahrens komplizierter als die Praxis. Deshalb geben wir einige typische Beispiele:
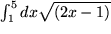 mit
mit 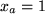 und
und 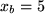 . Als neue Variable drängt sich
. Als neue Variable drängt sich 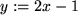 auf
aufmit
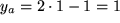 ,
, 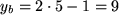 und
und 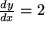 also
also 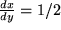 . Daraus folgt:
. Daraus folgt: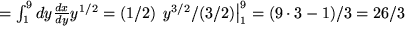 .
.
Ein für die Physik wichtiges Beispiel ist:
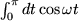 mit
mit 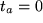 und
und 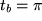 . Wir wählen die Substitution
. Wir wählen die Substitution 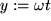
mit
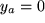 ,
, 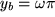 und
und 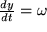 also
also 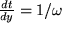 . Damit ergibt sich:
. Damit ergibt sich: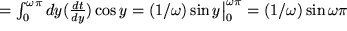 .
.
Noch ein drittes Beispiel aus der Physik:
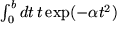 mit
mit 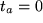 und
und  . Wir substituieren
. Wir substituieren 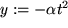
mit
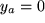 ,
, 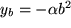 und
und 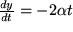 also
also 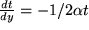 . Daraus erhalten wir:
. Daraus erhalten wir: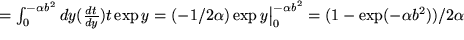 .
.
Ganze Klassen von Integralen erhält man auf folgende Weise durch Benützen der "Substitutionsformel rückwärts". Was damit gemeint ist, sieht man am besten an folgenden Beispielen:
Gesetzt den Fall wir haben ein Integral auszurechnen von folgendem Typ, wobei wir suggestiv für die willkürliche Intergrationsvariable 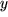 gewählt haben:
gewählt haben:
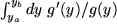
so bildet dies offensichtlich die rechte Seite unserer Substitutionsformel speziell für die Funktion 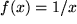 und wir können die Substitutionsformel sofort mit
und wir können die Substitutionsformel sofort mit 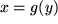 von rechts nach links, also "rückwärts" anwenden, um zu erhalten:
von rechts nach links, also "rückwärts" anwenden, um zu erhalten:

Das ist aber nach Zeile 14 unserer TABELLE gleich
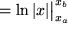
und mit 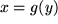 folgt insgesamt:
folgt insgesamt:
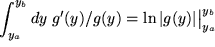
Als Beispiele erhalten wir etwa:
für 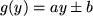 mit mit 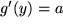 : : |
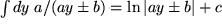 , , |
für 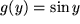 mit mit 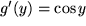 : : |
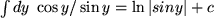 , , |
für 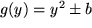 mit mit 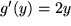 : : |
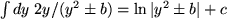 , usw. , usw. |
Ganz analog zeigt man mit  für
für 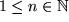 :
:
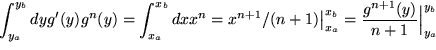
|
Aufgabe 7.6: Leiten Sie aus dieser Formel weitere ab, indem Sie |
|
Aufgabe 7.7: Beweisen Sie analog wie oben die Formel:
für |
|
Aufgabe 7.8: Was erhält man analog für |
|
Aufgabe 7.9: Weitere vermischte Beispiele zur Substitution:
|
Sie ahnen aus diesen Beispielen die ungeheure Menge und Vielfalt von Integralen, die durch Anwendung der Substitutionsformel berechnet werden können. Dennoch reicht das auch für die Zwecke der Physik immer noch lange nicht aus. Bei so einfachen Integranden wie 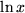 ,
, 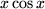 oder
oder 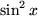 sind wir immer noch ratlos.
sind wir immer noch ratlos.
Für solche und ähnliche Fälle gibt es eine Methode, die uns das Integral zwar nicht ganz liefert, aber in gewissem Sinne wenigstens eine teilweise Berechnung gestattet und manchmal in mehreren Schritten dann doch zum Ziel führt. Diese Methode heißt sinnigerweise "partielle Integration".
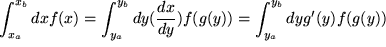
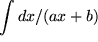
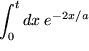
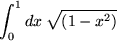
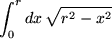
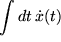
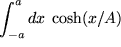
 spezifizieren:
spezifizieren: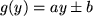
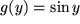
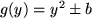
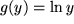 .
. 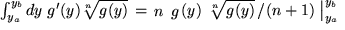
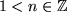 und spezifizieren Sie darin
und spezifizieren Sie darin 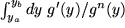 ?
?