Immer wenn ein Integrand so in ein Produkt 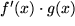 zerlegt werden kann, dass von einem der Faktoren
zerlegt werden kann, dass von einem der Faktoren 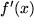 die Stammfunktion
die Stammfunktion  bekannt ist, sollte man die partielle Integration jedenfalls nicht unversucht lassen. Wir erinnern uns an die Produktregel der Differentiation aus Abschnitt 5.5.2:
bekannt ist, sollte man die partielle Integration jedenfalls nicht unversucht lassen. Wir erinnern uns an die Produktregel der Differentiation aus Abschnitt 5.5.2:
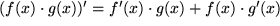
integrieren diese und benützen den zweiten Teil des Hauptsatzes zur Integration des Produkts:
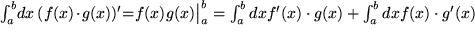
Nach dem ersten Term auf der rechten Seite aufgelöst, erhalten wir die Formel für die:
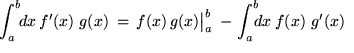
Das ist natürlich wegen des verbleibenden Integrals nach dem charakteristischen Minuszeichen auf der rechten Seite keine fertige Lösung unseres Problems. Aber manchmal ist dieses Integral leichter zu berechnen als das ursprüngliche.
Wir betrachten sogleich unsere oben genannten typischen Beispiele, etwa mit 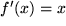 und
und 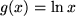 :
:
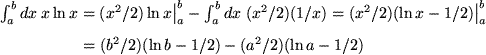
Oder noch ein anderes vielleicht unerwartetes, aber keineswegs seltenes Beispiel mit 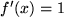 und
und 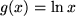 , bei dem durch das Einfügen einer Eins künstlich ein triviales Produkt erzeugt wurde:
, bei dem durch das Einfügen einer Eins künstlich ein triviales Produkt erzeugt wurde:
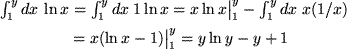
Es ist nicht immer leicht zu sehen, welchen Faktor des Produkts man zweckmäßigerweise als Ableitung 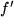 betrachtet. Dazu das Beispiel
betrachtet. Dazu das Beispiel 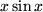 zunächst naheliegend mit
zunächst naheliegend mit 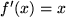 :
:
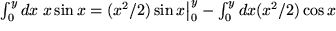
Man sieht sofort, dass uns diese Wahl nicht weiterbringt, sondern den verbleibenden Integranden nur noch komplizierter macht. Die andere Möglichkeit 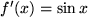 dagegen führt uns zum Erfolg:
dagegen führt uns zum Erfolg:
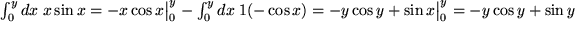
Wir betrachten noch den Integranden 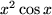 und wählen nach unseren soeben gemachten Erfahrungen
und wählen nach unseren soeben gemachten Erfahrungen 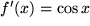 :
:
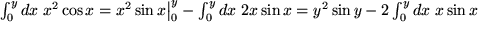
Das ist zwar nicht die Lösung unseres Problems, aber ein Schritt in die richtige Richtung, denn das verbleibende Integral haben wir als letztes Beispiel gerade ausgerechnet. Damit folgt:
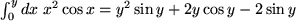
Insgesamt hat uns hier zweimalige partielle Integration zum Ziel geführt.
Ein weiteres interessantes Beispiel ist (zur Abwechslung mal als unbestimmtes Integral):
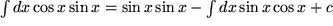
Das verbleibende Integral ist gleich dem ursprünglichen, folglich erhalten wir mit neuem  :
:

Auch das nächste Beispiel mit 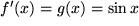 ist bemerkenswert:
ist bemerkenswert:
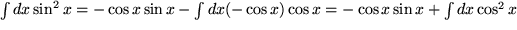
Nach Einsetzen der Relation 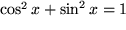 erhalten wir:
erhalten wir:
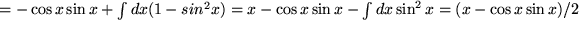
Hier folgt noch eine ganze Reihe von Beispielen dieser Art mit 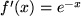 , für die wegen ihrer Bedeutung auch für die Physik sogar eine Bezeichnung festgelegt wurde:
, für die wegen ihrer Bedeutung auch für die Physik sogar eine Bezeichnung festgelegt wurde:
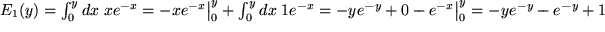
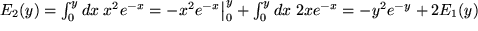 usw.
usw.
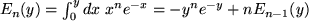
|
Aufgabe 7.10: Integrieren Sie folgende Integrale durch partielle Integration:
|
|
Aufgabe 7.11: Zeigen Sie, dass man bei einer geradlinigen Bewegung eines Massepunkts den zurückgelegten Weg 
|
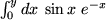
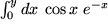
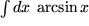
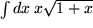
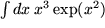
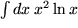
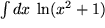
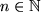 :
: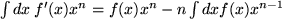
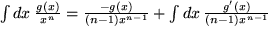 für
für 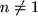
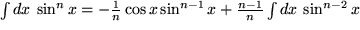
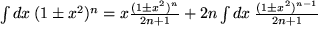
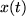 aus dem vorgegebenen Beschleunigungsverlauf
aus dem vorgegebenen Beschleunigungsverlauf 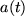 mit Anfangsgeschwindigkeit
mit Anfangsgeschwindigkeit 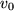 und -ort
und -ort  durch partielle Integration in folgender Form erhält:
durch partielle Integration in folgender Form erhält: