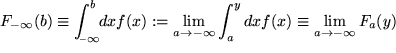7 Integration

7.6 Uneigentliche Integrale

7.6.1 Unendliches Integrationsintervall

Wenn z.B. das Integral über eine im Intervall stetige Funktion an der oberen Grenze bis ins Unendliche reichen soll, berechnet man dieses zunächst nur bis zu einem großen endlichen Wert und läßt dann nachträglich im Ergebnis der Integration diesen großen Wert in einem weiteren Grenzübergang über alle Grenzen wachsen. Falls auch dieser Grenzwert existiert, nennen wir ihn ein uneigentliches Integral der ersten Art und schreiben:

Als Beispiel berechnen wir für und ein kleines positives :

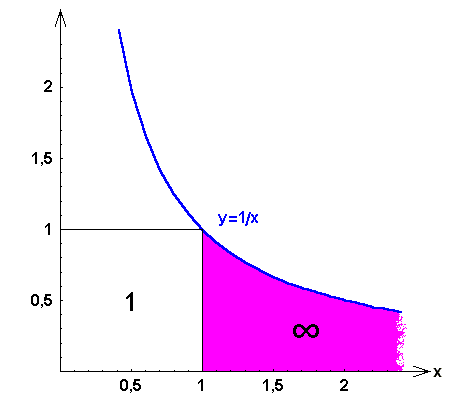
Wir sehen daraus, dass das uneigentliche Integral existiert, wenn die Funktion für wachsendes auch nur ein klein wenig stärker abfällt als , also z.B. für , dass aber für die im folgenden Bild

Bild 7.12

farbige Fläche unter der Funktion gerade keinen endlichen Flächeninhalt mehr besitzt und ebenso alle weniger stark abfallenden Funktionen wie etwa .

Analog verfahren wir bei einer in stetigen und beschränkten Funktion für die untere Grenze:

oder bei einer auf der ganzen Zahlengeraden stetigen und beschränkten Funktion für beide Grenzen:

mit einer beliebigen Teilungsstelle .