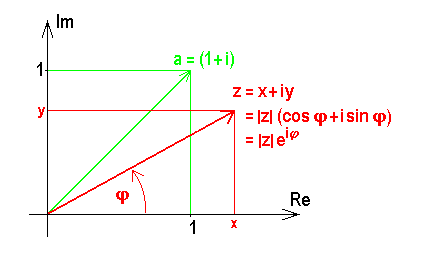8 Komplexe Zahlen

8.1 Imaginäre Einheit und Darstellungen

8.1.4 Gaußsche Zahlenebene

Zur Darstellung eines geordneten Paars reeller Zahlen bietet sich natürlich die Ebene an, die wir schon bei der Darstellung von Variable und Funktionswert einer reellen Funktion verwendet haben und jetzt Gaußsche Zahlenebene nennen: jedem Punkt (oder "Zeiger", wie die Elektrotechniker sagen) der Gaußschen Zahlenebene entspricht also genau eine komplexe Zahl.

Als Orientierungshilfe zeichnen wir in der Ebene zwei reelle Zahlengeraden aus, die aufeinander senkrecht stehen, die reelle Achse und die imaginäre Achse , d.h. wir wählen ein kartesisches Koordinatensystem: der Realteil einer komplexen Zahl , d.h. eines Punktes (oder Zeigers) , ist dann die Projektion seines Abstands vom Nullpunkt (oder seiner Länge) auf die reelle 1-Achse, und der Imaginärteil entsprechend auf die imaginäre 2-Achse, wie im folgenden Bild zu sehen:

Bild 8.1: Gaußsche Zahlenebene mit kartesischem Koordinatensystem

Als Alternative zu kartesischen Koordinaten in den Ebene kann man selbstverständich auch ebene Polarkoordinaten verwenden, indem man

schreibt mit dem

Daraus folgt nach dem Pythagoras für den

Der Polarwinkel, den man man aus erhält, ist nur bis auf additive Terme bestimmt und heißt

Bei der Bestimmung des Arguments stößt man auf eine kleine Schwierigkeit, eine Zweideutigkeit, die daher kommt, dass :
Wenn wir z.B. die komplexe Zahl betrachten mit dem Realteil und dem Imaginärteil , erhalten wir für den Betrag zwar eindeutig , für das Argument jedoch zunächst zwei Werte oder , die beide im Intervall liegen. Durch Einsetzen der beiden in Frage kommenden Werte in können wir jedoch in jedem Fall leicht das richtige Argument finden: für erhalten wir richtig: , während uns das falsche Resultat liefert.