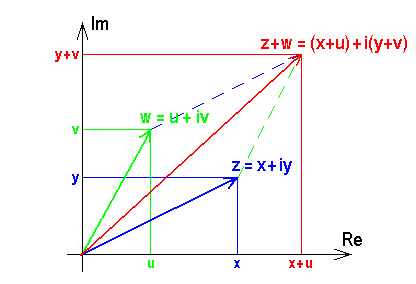
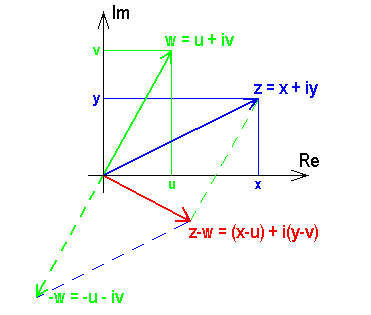Die komplexen Zahlen bilden wie die reellen eine abelsche Gruppe der Addition: Wenn 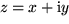 und
und 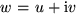 zwei komplexe Zahlen sind, dann ist ihre Summe:
zwei komplexe Zahlen sind, dann ist ihre Summe:
Die Veranschaulichung in der Gauß-Ebene erfolgt am besten mit Hilfe des kartesischen Koordinatensystems: Der "Zeiger" der Summe ist das, was die Physiker aus dem Kräfteparallelogramm als resultierende Kraft kennen, wie im nächsten Bild zu sehen:
Der Betrag der Differenz 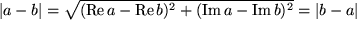 ist der Abstand der beiden entsprechenden Punkte bzw. der Spitzen der entsprechenden Zeiger in der Ebene.
ist der Abstand der beiden entsprechenden Punkte bzw. der Spitzen der entsprechenden Zeiger in der Ebene.
Insbesondere gilt die Dreiecksungleichung: 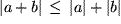 .
.
Für die komplexen Zahlen selbst gibt es keine Ungleichungen mehr. Man kann offenbar für zwei beliebige komplexe Zahlen nicht mehr entscheiden, welche von ihnen die größere ist. Das ist der wichtige Unterschied zu den auf der Zahlengeraden angeordneten reellen Zahlen und der Preis, den wir für die Erweiterung zahlen mußten. Es gibt allerdings noch einen "Rest von Ordnung", nämlich aus 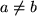 folgt immer noch
folgt immer noch 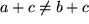 .
.
Das komplex Konjugierte einer Summe ist die Summe der konjugierten Summanden:
Der Stern kann also in die Klammer hineingezogen werden.
Aus der Summe bzw. Differenz einer komplexen Zahl und ihrer komplex Konjugierten erhält man leicht den Real- bzw. Imaginärteil:
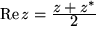
bzw.
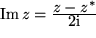
Die komplex Konjugierte 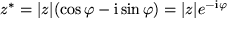 gestattet uns so auch die Umkehrung der Euler-Formel:
gestattet uns so auch die Umkehrung der Euler-Formel:

und
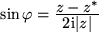
.
![]() und
und ![]() zwei komplexe Zahlen sind, dann ist ihre Summe:
zwei komplexe Zahlen sind, dann ist ihre Summe: