Ganz analog wie im Reellen definieren wir komplexe Funktionen einer komplexen Variablen
wieder als Input-Output-Relation oder Abbildung, jedoch mit einem bedeutenden Unterschied
: Die dort ausdrücklich in den Funktionsbegriff mit eingeschlossenen
Eindeutigkeit mit
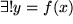 wollen wir bei den komplexen Funktionen nicht voraussetzen:
wollen wir bei den komplexen Funktionen nicht voraussetzen:
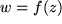 komplexe Funktion:
komplexe Funktion:
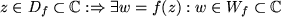
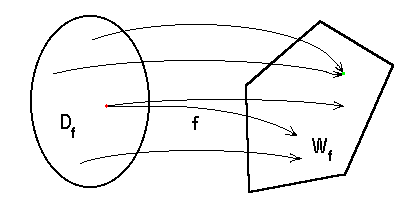
Bild 8.8: Komplexe Funktion mit Mehrwertigkeit
Es wird also möglich und sogar die Regel sein, dass es zu einem Wert der unabhängigen
komplexen Variablen
 aus dem Definitionsbereich
aus dem Definitionsbereich
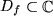 im Wertevorrat
im Wertevorrat
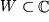 mehrere Funktionswerte
mehrere Funktionswerte
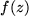 gibt.
Wir werden ein-, zwei-, drei- usw. mehrdeutige, besser mehrwertige
Funktionen kennen lernen und sogar
gibt.
Wir werden ein-, zwei-, drei- usw. mehrdeutige, besser mehrwertige
Funktionen kennen lernen und sogar
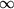 -wertige zulassen.
-wertige zulassen.
Auf eine wichtige komplexe Funktion, die Exponentialfunktion, sind wir im Abschnitt 8.1.5 bereits gestoßen.
Da wir bei den komplexen Zahlen keine Ordnung mehr haben, kann es natürlich kein Analogon zur Monotonie geben, die für reelle Funktionen sehr wichtig war.
Das Rechnen mit komplexen Funktionen einer komplexen Variablen erfolgt nach
den im letzten Abschnitt zusammengestellten Regeln des Körpers
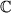 mit den beiden Kommutativen und Assoziativen Gesetzen sowie dem verbindenden
Distributiven Gesetz: Z.B. ergibt die Summe bzw. Differenz zweier komplexer Funktionen
mit den beiden Kommutativen und Assoziativen Gesetzen sowie dem verbindenden
Distributiven Gesetz: Z.B. ergibt die Summe bzw. Differenz zweier komplexer Funktionen
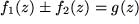 eine neue komplexe Funktion, das komplexe Vielfache
eine neue komplexe Funktion, das komplexe Vielfache
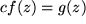 mit
mit
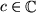 ebenfalls und analog das Produkt
ebenfalls und analog das Produkt
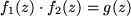 oder, falls
oder, falls
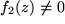 im Definitionsbereich,
auch der Quotient
im Definitionsbereich,
auch der Quotient 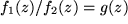 .
.