9 Vektoren
9.1 Dreidimensionaler euklidischer Raum
9.1.4 Transformationen des Koordinatensystems
Hoffentlich haben Sie gemerkt, wie willkürlich wir bei der Wahl des Koordinatensystems vorgegangen sind. Da ein geschickt gewähltes Koordinatensystem für die tägliche Arbeit der Physiker außerordentlich bequem sein kann, die Willkür bei der Wahl aber und die Unabhängigkeit der Resultate der physikalischen Messungen von dieser Wahl von überragender Bedeutung sind, wollen wir uns noch etwas damit beschäftigen, was passiert wäre, wenn wir eine andere Wahl getroffen hätten:
Besonders vier Arten von Transformationen des Koordinatensystems sind praktisch interessant. Wir wählen jeweils ein einfaches, aber typisches Beispiel aus:
1) TRANSLATIONEN (VERSCHIEBUNGEN), z.B. um die Strecke 1 cm in 3-Richtung:
Zunächst beschäftigt uns die Willkür bei der Wahl des Ursprungs: Wie sähen die Koordinaten 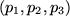 des Punktes
des Punktes 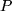 aus, wenn wir statt des Punktes
aus, wenn wir statt des Punktes 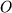 einen anderen Punkt, z.B.
einen anderen Punkt, z.B. 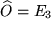 , als Nullpunkt gewählt hätten, der um die Strecke
, als Nullpunkt gewählt hätten, der um die Strecke 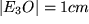 in positiver 3-Richtung verschoben ist?
in positiver 3-Richtung verschoben ist?
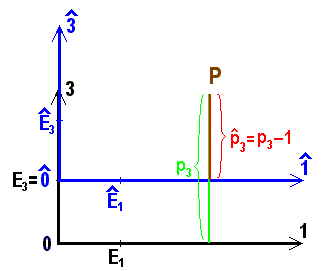
Bild 9.4: Translation um die Strecke 1 cm in positive 3-Richtung
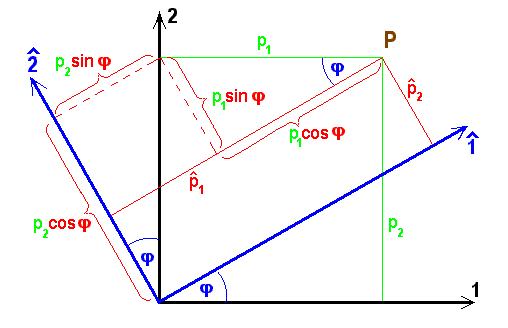
Bild 9.5: Drehung des Koordinatensystems um den Winkel 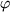 um die 3-Richtung
um die 3-Richtung
Aus dem Bild entnehmen wir, dass 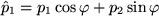 und
und 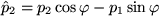 , während
, während 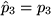 , also:
, also:
z.B. ergibt sich für 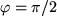 :
: 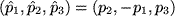 ,
,
Weitere sehr interessante Transformationen, die den Nullpunkt invariant lassen, sind die
3) SPIEGELUNGEN, z.B. am Ursprung (Paritätstransformation).
Es genügt, eine einzige Spiegelung zu betrachten, da man alle anderen aus dieser und geeigneten Drehungen zusammensetzen kann. Wir wählen dazu die Punktspiegelung am Ursprung, die im folgenden Bild veranschaulicht und bei den Physikern unter dem Namen Paritätstransformation bekannt ist:
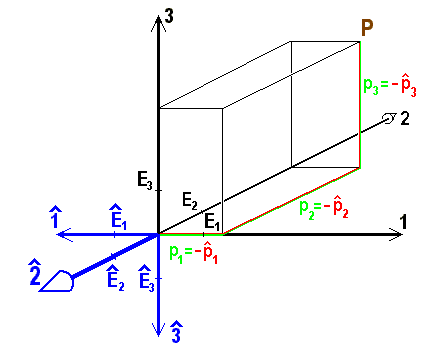
Bild 9.6: Spiegelung des Koordinatensystems am Ursprung
Wir wissen und sehen sofort aus dem Bild, dass dabei alle Koordinaten in ihr Negatives übergehen:
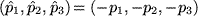
.
|
Aufgabe 9.4: Spiegelungen aus Parität und Drehungen
Zeigen Sie, wie man die Spiegelung an der 1-2-Ebene, bei der 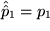 , , 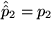 und und 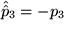 , aus der Paritätstransformation und einer Drehung erhalten kann. Lösung , aus der Paritätstransformation und einer Drehung erhalten kann. Lösung
|
Alle Spiegelungen und speziell die Paritätstransformation haben eine bemerkenswerte Eigenschaft, die wir leicht aus dem obigen Bild erkennen: Wenn wir nämlich die positive Hälfte der 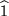 -Achse um den Winkel
-Achse um den Winkel 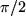 in die positive Hälfte der
in die positive Hälfte der 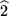 -Achse drehen, dann ist das in Richtung der positiven
-Achse drehen, dann ist das in Richtung der positiven 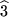 -Achse gesehen keine Rechtsschraube mehr, sondern eine Linksschraube (mit Antiuhrzeigersinn). D.h. nach einer Spiegelung ist aus unserem Rechtskoordinatensystem ein Linkskoordinatensystem geworden. Für Leute, die sich auf die Verwendung von Rechtskoordinatensystemen geeinigt haben, ist das keine erfreuliche Sache, aber wir müssen lernen, damit zu leben und Mittel und Wege zu finden, auch eine versteckte Spiegelung immer sofort zu entlarven, wenn wir bei Rechtskoordinatensystemen bleiben wollen.
-Achse gesehen keine Rechtsschraube mehr, sondern eine Linksschraube (mit Antiuhrzeigersinn). D.h. nach einer Spiegelung ist aus unserem Rechtskoordinatensystem ein Linkskoordinatensystem geworden. Für Leute, die sich auf die Verwendung von Rechtskoordinatensystemen geeinigt haben, ist das keine erfreuliche Sache, aber wir müssen lernen, damit zu leben und Mittel und Wege zu finden, auch eine versteckte Spiegelung immer sofort zu entlarven, wenn wir bei Rechtskoordinatensystemen bleiben wollen.
Als letztes Beispiel für die Transformation des Koordinatensystems untersuchen wir
4) STRECKUNGEN (DILATATIONEN): speziell aller drei Achsen um einen gemeinsamen Faktor, z.B. 10:
Etwas Derartiges kommt in der Praxis etwa vor, wenn wir dazu übergehen wollen, Längen statt in Zentimetern cm in Dezimetern dm zu messen. Bei solch einer Maßstabsänderung bleibt selbstverständlich der Ursprung invariant und auch die Koordinatenachsen bleiben unverändert, nur die Maß-Punkte 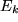 werden auf den Achsen so verschoben, dass
werden auf den Achsen so verschoben, dass 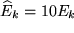 , also die Abstände vom Ursprung
, also die Abstände vom Ursprung 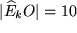 vergrößert werden:
vergrößert werden:
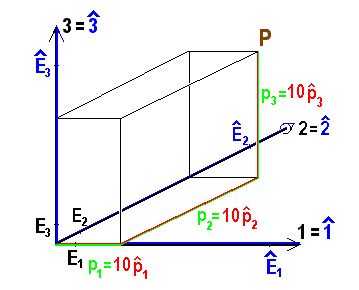
Bild 9.7: Maßstabsänderung des Koordinatensystems um einen Faktor 10
Wenn Sie die Tastatur Ihres PC statt in cm in größeren Einheiten, z.B. dm messen, erhalten Sie natürlich kleinere Maßzahlen, nämlich:
Zusammenfassend können wir feststellen, dass die Koordinaten ein und desselben Punktes 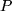 in verschiedenen Koordinatensystemen beträchtlich verschieden sind, dass wir also im folgenden immer auf die Koordinatensysteme achten müssen, wenn wir physikalische Zustände und Vorgänge beschreiben wollen.
in verschiedenen Koordinatensystemen beträchtlich verschieden sind, dass wir also im folgenden immer auf die Koordinatensysteme achten müssen, wenn wir physikalische Zustände und Vorgänge beschreiben wollen.
Bisher sind wir jedoch erst bei den Punkten des dreidimensionalen euklidischen Raumes, können also nur ein statisches "Stillleben" von Massen, Ladungen, usw. beschreiben. Die Physik wird jedoch erst richtig interessant, wenn Bewegung in die Sache kommt.
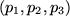 des Punktes
des Punktes 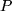 aus, wenn wir statt des Punktes
aus, wenn wir statt des Punktes 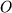 einen anderen Punkt, z.B.
einen anderen Punkt, z.B. 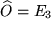 , als Nullpunkt gewählt hätten, der um die Strecke
, als Nullpunkt gewählt hätten, der um die Strecke 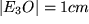 in positiver 3-Richtung verschoben ist?
in positiver 3-Richtung verschoben ist?
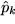 gilt:
gilt: 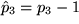 , während
, während 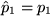 und
und 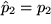 unverändert bleiben, also insgesamt:
unverändert bleiben, also insgesamt: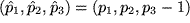
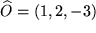 liegt?
liegt? 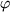 um die 3-Richtung:
um die 3-Richtung: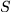 ein neues
ein neues 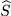 , das bei gleichbleibendem Ursprung
, das bei gleichbleibendem Ursprung 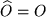 z.B. um einen Winkel
z.B. um einen Winkel 
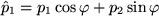 und
und 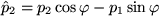 , während
, während 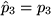 , also:
, also: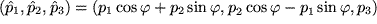
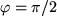 :
: 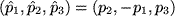 ,
,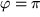
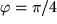
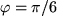

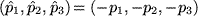 .
.
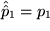 ,
, 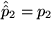 und
und 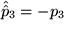 , aus der Paritätstransformation und einer Drehung erhalten kann.
, aus der Paritätstransformation und einer Drehung erhalten kann. 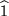 -Achse um den Winkel
-Achse um den Winkel 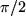 in die positive Hälfte der
in die positive Hälfte der 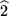 -Achse drehen, dann ist das in Richtung der positiven
-Achse drehen, dann ist das in Richtung der positiven  -Achse gesehen keine Rechtsschraube mehr, sondern eine Linksschraube (mit Antiuhrzeigersinn). D.h. nach einer Spiegelung ist aus unserem Rechtskoordinatensystem ein Linkskoordinatensystem geworden. Für Leute, die sich auf die Verwendung von Rechtskoordinatensystemen geeinigt haben, ist das keine erfreuliche Sache, aber wir müssen lernen, damit zu leben und Mittel und Wege zu finden, auch eine versteckte Spiegelung immer sofort zu entlarven, wenn wir bei Rechtskoordinatensystemen bleiben wollen.
-Achse gesehen keine Rechtsschraube mehr, sondern eine Linksschraube (mit Antiuhrzeigersinn). D.h. nach einer Spiegelung ist aus unserem Rechtskoordinatensystem ein Linkskoordinatensystem geworden. Für Leute, die sich auf die Verwendung von Rechtskoordinatensystemen geeinigt haben, ist das keine erfreuliche Sache, aber wir müssen lernen, damit zu leben und Mittel und Wege zu finden, auch eine versteckte Spiegelung immer sofort zu entlarven, wenn wir bei Rechtskoordinatensystemen bleiben wollen.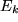 werden auf den Achsen so verschoben, dass
werden auf den Achsen so verschoben, dass 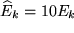 , also die Abstände vom Ursprung
, also die Abstände vom Ursprung 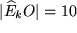 vergrößert werden:
vergrößert werden: