Matrizen:
Die Drehmatrizen sind nur ein Beispiel für die Größen mit zwei Indizes, die die Mathematiker Matrizen nennen.
Man kann ganz allgemein für
![]() -Matrizen,
d.h. Schemata mit
-Matrizen,
d.h. Schemata mit ![]() Zeilen und
Zeilen und
![]() Spalten Rechenregeln definieren und deren Strukturen untersuchen. Wir wollen unsere Überlegungen hier auf
quadratischen
Spalten Rechenregeln definieren und deren Strukturen untersuchen. Wir wollen unsere Überlegungen hier auf
quadratischen
![]() -Matrizen und sogar speziell auf
-Matrizen und sogar speziell auf
![]() -Matrizen mit reellen Elementen beschränken.
-Matrizen mit reellen Elementen beschränken.
Wir bezeichnen die Matrizen durch unterstrichene große Buchstaben z.B.
![]() . Ihre Elemente
. Ihre Elemente
![]() tragen zwei
Indizes: der linke
tragen zwei
Indizes: der linke
![]() bezeichnet die
(waagrechte) Zeile und der rechte
bezeichnet die
(waagrechte) Zeile und der rechte
![]() die (senkrechte)
Spalte der Matrix:
die (senkrechte)
Spalte der Matrix:

Es gibt einige Arten von Matrizen die ihrer Wichtigkeit wegen besondere Namen haben:
Vor allem Diagonalmatrizen, bei denen nur die drei Elemenete
![]() ,
,
![]() und
und
![]() in der
sogenannten Hauptdiagonale (:von links oben nach rechts unten) von
in der
sogenannten Hauptdiagonale (:von links oben nach rechts unten) von
![]() verschieden sind,
haben besondere Bedeutung. Die Nebendiagonale (:von rechts oben nach links unten) ist im Vergleich dazu weniger
wichtig.
verschieden sind,
haben besondere Bedeutung. Die Nebendiagonale (:von rechts oben nach links unten) ist im Vergleich dazu weniger
wichtig.

Die Matrizen für Drehungen um Vielfache des Winkels
![]() sind Beispiele für
Diagonalmatrizen:
sind Beispiele für
Diagonalmatrizen: ![]() ,
,
![]() und
und
![]() .
.
Auf halbem Weg zur Diagonalgestalt ist die Dreiecksform zu erwähnen, bei der entweder unter oder über der Hauptdiagonale nur Nullen stehen:

Auch Matrizen in Kästchenform sind für viele Zwecke besonders angenehm. Bei ihnen sind nur
"Kästchen" um die Hauptdiagonale von Null verschieden. Unsere Drehmatrizen
![]() und
und
![]() sind von dieser Art.
sind von dieser Art.

Eine einfache Operation, die bei jeder Matrix durchgeführt werden kann, ist die Transposition:
Gemeint ist die Spiegelung der Matrixelemente an der Hauptdiagonale, bzw. die Vertauschung der
Zeilen mit den Spalten:
![]()

Es gibt Matrizen, bei denen die Transposition nichts ändert: Man nennt sie symmetrisch.
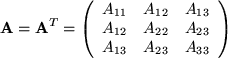
Diese symmetrischen Matrizen treten in der Physik häufig auf und haben den Vorteil, dass man sie mit bestimmten einfachen Umformungen auf Diagonalgestalt bringen kann.
Wie Sie unmittelbar sehen, hat eine symmetrische Matrix nur sechs unabhängige Elemente.
Falls die Spiegelung an der Hauptdiagonale ein Minuszeichen ergibt, heißt die Matrix antisymmetrisch:
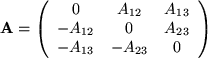
Die Diagonalelemente müssen in diesem Fall natürlich verschwinden. Offensichtlich besitzt eine
antisymmetrische
![]() -Matrix nur
genau drei unabhängige Elemente. Das ist der tiefere Grund für die Existenz eines Vektorprodukts in drei
Dimensionen, wie wir bald genauer sehen werden.
-Matrix nur
genau drei unabhängige Elemente. Das ist der tiefere Grund für die Existenz eines Vektorprodukts in drei
Dimensionen, wie wir bald genauer sehen werden.
Schließlich folgt noch ein Spezialausdruck für eine charakteristische Größe jeder quadratischen Matrix: Die Summe der Elemente in der Hauptdiagonalen heißt Spur (:englisch Trace) der Matrix:
Sie können sich leicht vorstellen, dass man für die reellen
![]() -Matrizen eine
gliedweise Addition definieren kann und dass diese dann eine abelsche Gruppe der Addition bilden mit
Assoziativgesetz, eindeutiger Nullmatrix, genau einem Negativen zu jeder Matrix und Kommutativem Gesetz, weil
sich die entsprechenden Eigenschaften der reellen Zahlen einfach übertragen. Auch die elementweise
Multiplikation mit einem Zahlenfaktor ist möglich und führt zu den üblichen Distributivgesetzen.
-Matrizen eine
gliedweise Addition definieren kann und dass diese dann eine abelsche Gruppe der Addition bilden mit
Assoziativgesetz, eindeutiger Nullmatrix, genau einem Negativen zu jeder Matrix und Kommutativem Gesetz, weil
sich die entsprechenden Eigenschaften der reellen Zahlen einfach übertragen. Auch die elementweise
Multiplikation mit einem Zahlenfaktor ist möglich und führt zu den üblichen Distributivgesetzen.
Für die Physik viel wichtiger ist jedoch die Multiplikation zweier
![]() -Matrizen,
was im Spezialfall der Transformationsmatrizen zwei hintereinander ausgeführten Transformationen des
Koordinatensystems entspricht:
-Matrizen,
was im Spezialfall der Transformationsmatrizen zwei hintereinander ausgeführten Transformationen des
Koordinatensystems entspricht:
Dabei gilt folgende
|
Matrizenmultiplikationsvorschrift:
|
Bei der letzten angegebenen Formulierung wurde nach der Einsteinschen Summenkonvention (Siehe Abschnitt 9.2.3.2) das Summenzeichen weggelassen, weil die beiden gleichlautenden Indizes k die Summation genügend deutlich signalisieren.
In der Praxis denkt man sich zur Berechnung des Produktmatrixelements
![]() der z-ten Zeile und der s-ten Spalte die s-te (senkrechte) Spalte
der z-ten Zeile und der s-ten Spalte die s-te (senkrechte) Spalte
![]() der rechten Faktormatrix
der rechten Faktormatrix
![]() waagrecht auf die z-te Zeile
waagrecht auf die z-te Zeile
![]() der linken
Faktormatrix
der linken
Faktormatrix
![]() gelegt,
aufeinanderliegende Elemente miteinander multipliziert und die drei Produkte addiert: z.B.
gelegt,
aufeinanderliegende Elemente miteinander multipliziert und die drei Produkte addiert: z.B.
![]() , also insgesamt:
, also insgesamt:
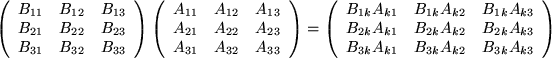
|
Aufgabe 9.10: Matrizenmultiplikation Multiplizieren Sie folgende Transformations-Matrizen:
|
Die wichtigste Entdeckung bei der Bearbeitung der Übungsaufgabe 9.10 ist, dass im allgemeinen für zwei Drehungen und folglich auch für die darstellenden Matrizen kein Kommutatives Gesetz gilt. Diese Tatsache können Sie mit jeder Streichholzschachtel leicht und anschaulich überprüfen, wie im folgenden Bild illustriert:
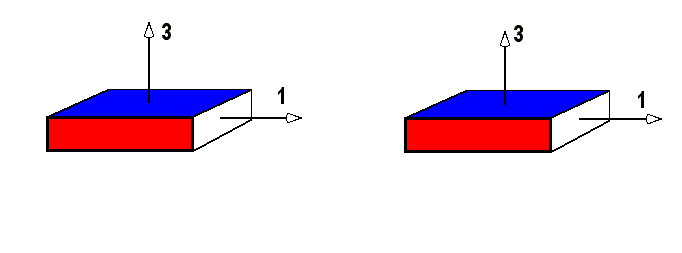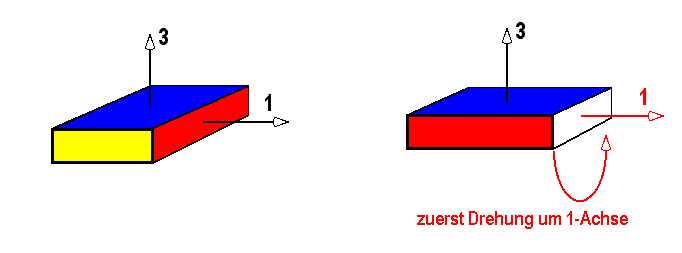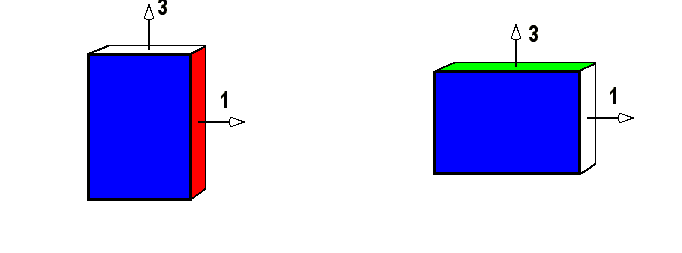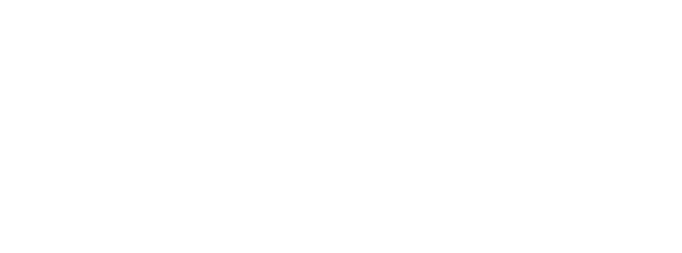
Bild 9.10: Streichholzschachtel, die zuerst um
![]() um die
3-Achse, dann um
um die
3-Achse, dann um ![]() um die 1-Achse gedreht wurde, verglichen mit einer, die zuerst um die 1-Achse und dann um die 3-Achse gedreht
wurde.
um die 1-Achse gedreht wurde, verglichen mit einer, die zuerst um die 1-Achse und dann um die 3-Achse gedreht
wurde.
Die Beispiele der Aufgabe 9.10 haben Ihnen jedoch auch schon gezeigt, dass in einigen Ausnahmefällen
das Kommutative Gesetz doch gilt: Z.B. sind alle Drehungen um ein und dieselbe Achse vertauschbar.
Auch Diagonalmatrizen sind miteinander vertauschbar. Das ist ein Grund für ihre Beliebtheit. Wenn
![]() ist, dann
verspricht die sogenannte Vertauschungsrelation
ist, dann
verspricht die sogenannte Vertauschungsrelation
![]() eine
interessante Größe zu sein. Das wird später in der Quantenmechanik noch große Bedeutung gewinnen.
eine
interessante Größe zu sein. Das wird später in der Quantenmechanik noch große Bedeutung gewinnen.
Von der Kommutativität abgesehen, verhält sich die Matrizenmultiplikation jedoch, wie wir das erwarten: Sie befolgt ein
|
Aufgabe 9.11: Assoziativgesetz bei Matrizenmultiplikation Verifizieren Sie das Assoziative Gesetz an der Euler-Drehung:
|
Es existiert eine eindeutig bestimmte
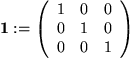 mit
mit
unabhängig davon, ob von rechts oder von links multipliziert wird.
Nur bei der
gibt es eine gewisse Komplikation ähnlich der Bedingung
![]() bei der
Division durch eine reelle Zahl. Eine eindeutig bestimmte Inverse gibt es nur für sogenannte
nichtsinguläre Matrizen. Das sind Matrizen, deren
Determinante nicht verschwindet:
bei der
Division durch eine reelle Zahl. Eine eindeutig bestimmte Inverse gibt es nur für sogenannte
nichtsinguläre Matrizen. Das sind Matrizen, deren
Determinante nicht verschwindet:
![]() .
Mit den Determinanten, dem wichtigsten Charakteristikum jeder Matrix, beschäftigen wir uns in einer
gesonderten Schublade.
.
Mit den Determinanten, dem wichtigsten Charakteristikum jeder Matrix, beschäftigen wir uns in einer
gesonderten Schublade.
Für unsere Transformationsmatrizen ist diese Einschränkung jedoch bedeutungslos. Für sie ist nämlich die
inverse Matrix einfach gleich der transponierten
![]() ,
die, wie wir gesehen haben, immer existiert: Man nennt eine derartige Matrix orthogonal
(Siehe Abschnitt 9.8.2) und wir werden uns diese noch
besonders ansehen:
,
die, wie wir gesehen haben, immer existiert: Man nennt eine derartige Matrix orthogonal
(Siehe Abschnitt 9.8.2) und wir werden uns diese noch
besonders ansehen: