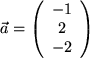Einheitsvektoren sind dimensionslose Vektoren der Länge 1, die je eine Richtung im Raum kennzeichnen. Man erhält aus einem beliebigen Vektor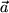 
den zu der entsprechenden Richtung gehörenden Einheitsvektor durch Division durch die Länge 
, bzw. Multiplikation mit 
:
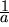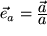oder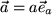 
.
|
Aufgabe 9.18: Einheitsvektoren
|
Wir verwenden im folgenden durchweg die drei Einheitsvektoren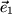 
, 
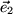und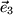 
als Basisvektoren, wobei 
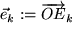. Die drei auf Länge eins normierten Basisvektoren 
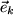werden manchmal auch Dreibein genannt.
Nachdem wir die Vektorkomponenten als Teilverschiebungsstrecken entlang der Koordinatenachsen (oder dazu äquivalent als Projektionen der Länge des Vektors auf die Koordinatenachsen) eingeführt haben, folgt unmittelbar:
( 
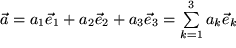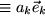mit Einsteinscher Summenkonvention! ).
Da wir zu Beginn dieses Kapitels nicht irgendein schiefwinkliges, sondern ein kartesisches Koordintensystem gewählt haben, wissen wir jedoch, dass die drei Einheitsvektoren 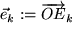paarweise aufeinander senkrecht stehen, also eine orthonormierte (d.h. orthogonale und normierte) Basis (ONB) darstellen. Um diese Tatsache in Formeln ausdrücken zu können, brauchen wir eine Größe, die mit dem Winkel zwischen zwei Vektoren zusammenhängt, die z.B. sagt, dass bei einem rechten Winkel zwischen zwei Vektoren die Projektion des einen auf den anderen verschwindet. Diese Aufgabe führt uns zur Frage nach der Multiplikation zweier Vektoren, die wir im nächsten Abschnitt behandeln werden.