Unter den Mehrfachprodukten aus vier Vektoren wird das Skalarprodukt zweier Vektorprodukte am häufigsten gebraucht. Z.B. ist das Skalarprodukt zweier Drehimpulse von dieser Struktur oder auch schon das Quadrat eines Drehimpulses.
Wir berechnen allgemein für die vier Vektoren
,
,
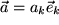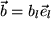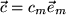und
(jeweils mit Summenkonvention!):
, d.h.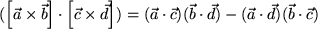
Dabei haben wir zunächst die Komponentendarstellung der beiden Vektorprodukte eingesetzt, die Homogenität des Skalarprodukts ausgenützt, die Orthonormalitätsrelation der Basisvektoren verwendet, über 
summiert, das Produkt der beiden einfach summierten Levi-Civita-Symbole durch Kronecker-Symbole ausgedrückt und schließlich das Ganze durch Ausführen der vier restlichen Summationen auf Skalarprodukte zurückgeführt.
Ein berühmter Spezialfall dieser Relation für
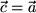und
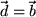ist die sogenannte
|
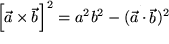
Aufgabe 9.46: Trägheitsmoment Bei der Definition des Trägheitsmoments setzt Ihr Dozent ohne Kommentar |
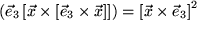. Darf er das?