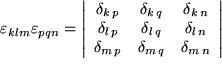
Zwei Levi-Civita-Symbole:
Für die Berechnung der weiteren Mehrfachprodukte benötigen wir das folgende Produkt von zwei Levi- Civita-Symbolen
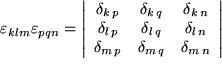
Der Beweis ist eine gute Übung in der Matrizenmultiplikation:
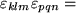
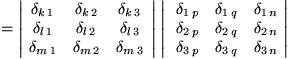
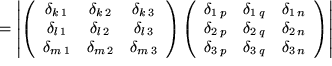
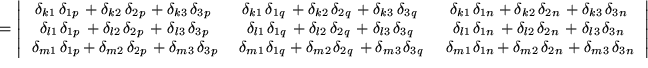
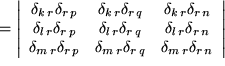
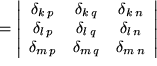
Zunächst haben wir die beiden Levi-Civita-Symbole durch zwei geschickt gewählte Determinantendarstellungen ersetzt, dann ausgenutzt, dass die Determinante des Produkts zweier Matrizen gleich dem Produkt der beiden Determinanten ist. Darauf haben wir die beiden Matrizen miteinander multipliziert, wie wir das früher gelernt haben. Die einzelnen Matrixelemente erweisen sich als Summen über jeweils drei Produkte von zwei Kronecker-Symbolen, die wir zusammenfassen und mit der Summenkonvention als Summen über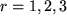 
schreiben können. Schließlich führen wir diese Summen aus, wobei jeweils nur ein einziges Kronecker- Symbol übrigbleibt.
Nachdem wir das Ergebnis vor uns haben, erkennen wir natürlich angesichts der Symmetrieeigenschaften der Determinanten, dass es nicht anders hätte ausfallen können, wenn wir bedenken, dass es notwendgerweise wie unser Ausgangsprodukt total antisymmetrisch in beiden Indextripeln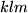 
und 
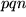sowie symmetrisch gegen Vertauschen der Indexpaare 
, 
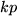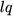und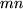 
sein muß.
Günstigerweise braucht man dieses allgemeine Ergebnis nur ganz selten. Meist wird das Produkt nur in dem Spezialfall benötigt, bei dem über ein Indexpaar, z.B. m, summiert ist:
|
|
Auch für diese wichtige Relation wollen wir zeigen, wie sie zustandekommt:
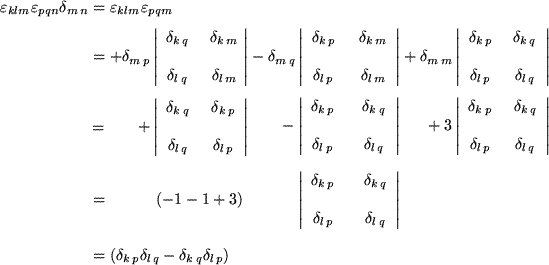
Wir haben dazu zunächst in der Determinantendarstellung des Produkts der Levi-Civita-Symbole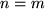 
gesetzt, die erhaltene 
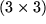-Determinante nach der letzten Zeile entwickelt und dann in den verbliebenen 
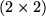-Determinanten die Summen über 
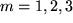ausgeführt, also insbesondere aus der Spur 
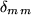eine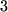 
erhalten. Nachdem wir in der ersten 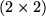-Determinante die beiden Spalten vertauscht hatten, stand das Ergebnis fest.
Die allgemeine Struktur, nämlich "antisymmetrisch in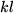 
und 
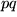sowie symmetrisch in 
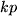und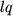 
und der Summationsindex 
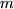darf nicht mehr vorkommen", hätte man erraten können, aber wir wären nicht sicher gewesen, dass der Zahlenfaktor vor dem Ganzen wirklich eine 
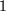ist.
Manchmal braucht man sogar nur das doppelt summierte Produkt der zwei Levi-Civita-Symbole, das wir nun ganz einfach erhalten können:
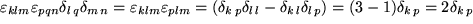
symmetrisch im Indexpaar 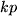, wie es sein muß. Zum Spaß summieren wir zum Schluß auch noch über das dritte Indexpaar:
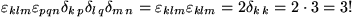
Analoge Relationen gibt es auch für die völlig summierten Levi-Civita-Symbole in Räumen anderer Dimensionen, z.B. im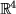 
, mit dem Ergebnis: "Dimension!"
