Wir schließen die Zerlegung der Mehrfachprodukte ab mit dem Vektorprodukt zweier Vektorprodukte. Dabei entscheiden wir uns dafür, zunächst das zweite innere Vektorprodukt möglichst lange unangetastet zu lassen:
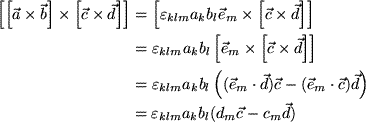
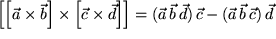 , d.h. koplanar mit
, d.h. koplanar mit 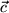 und
und 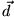 .
.
Wir haben dabei zunächst das erste Vektorprodukt durch seine Komponenten ersetzt, die Homogenität des Vektorprodukts ausgenützt, dann das erhaltene geschachtelte Vektorprodukt nach Graßmann entwickelt, die Projektion auf die Komponenten ausgeführt und schließlich Spatprodukte als Koeffizienten der beiden Faktorvektoren des zweiten Vektorprodukts erhalten, in deren Ebene das Ergebnis liegen muß.
Durch diese offensichtliche Unsymmetrie beunruhigt, berechnen wir dasselbe Produkt noch einmal, indem wir jetzt das erste innere Vektorprodukt möglichst lange unangetastet lassen und im übrigen ganz analog wie oben vorgehen:
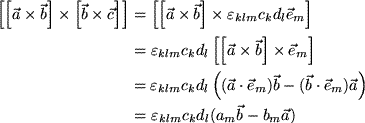
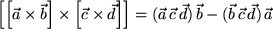 , d.h. koplanar mit
, d.h. koplanar mit 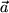 und
und 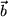 .
.
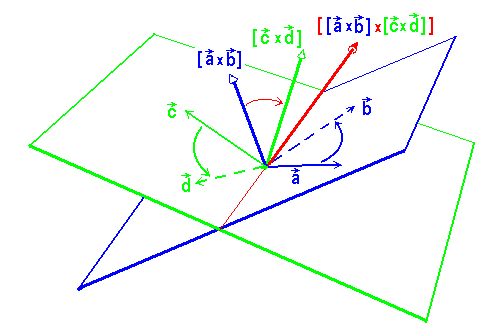
Der Produktvektor des Vektorprodukts zweier Vektorprodukte muß also auf der Schnittgeraden der von den beiden Faktorpaaren der inneren Vektorprodukte aufgespannten Ebenen liegen.
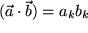 ,
, 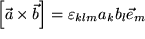 und
und 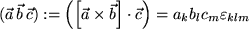 gilt:
gilt: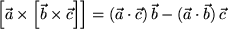
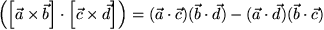
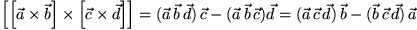
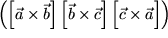 .
.