Determinanten-Formel:

Bei allen Transformationsüberlegungen werden Sie immer wieder folgende

verwenden. Die Relation sieht komplizierter aus, als sie in Wirklichkeit ist. Wir wollen uns kurz klarmachen, wie sie zustandekommt:

Wir betrachten dazu eine beliebige 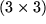-Matrix und bilden:

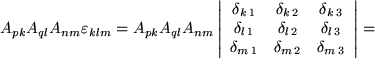
Wir haben zunächst das Levi-Civita-Symbol durch seine Determinantendarstellung mit Kronecker-Symbolen ersetzt und erinnern an die drei Summationen über 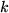, und 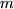. Da Determinanten reihenweise homogen sind, multipliziern wir die erste Zeile der Determinante mit dem ersten Faktor 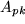, die zweite mit dem zweiten Faktor 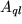und die dritte mit dem dritten Faktor 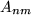. Dann führen wir die Summationen in allen neun Matrixelemeneten aus:

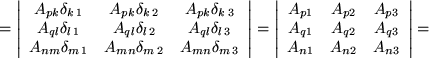
Nun machen wir die eben durchgeführten Summationen über die rechts stehenden Kronecker-Symbole wieder rückgängig, indem wir jedoch die Kronecker-Symbole jetzt links herausziehen. Danach stellen wir fest, dass wir die Determinante des Produkts zweier Matrizen erhalten haben:

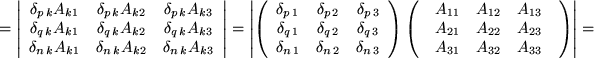
Die Determinante eines Matrizenprodukts ist jedoch gleich dem Produkt der Determinanten der beiden Faktoren.

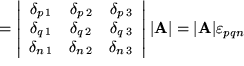
Damit haben wir das gewünschte Ergebnis erhalten, das Sie noch oft anwenden werden.

Da die gesamte Ableitung ebenso für die transponierte Matrix durchgeführt werden kann, wird die Determinaten-Formel häufig auch in folgender Form verwendet:

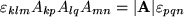
Unsere Determinanten-Formel 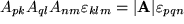kann noch auf eine ganz andere Art betrachtet werden: Das Levi-Civita-Symbol kann als Größe mit drei Indizes auch als Tensor dritter Stufe angesehen werden, und die linke Seite unserer Formel als 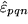, d.h. als Darstellung der 27 Tensorkomponenten im transformierten Koordinatensystem: für jeden Index eine Transformationsmatrix. So gesehen bedeutet dann 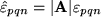die Drehinvarianz der Tensorkomponenten, d.h. die 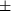Einsen und Nullen sind in jedem Koordinatensysem dieselben, und dazu kommt von 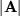ein Minuszeichen bei Spiegelungen., also handelt es sich um einen Pseudotensor. Dementsprechend werden Sie dem gegen Vertauschen je zweier Indizes total antisymmetrische Levi-Civita-Symbol manchmal auch als "numerisch drehinvariantem Pseudotensor dritter Stufe" begegnen.

Zurück zum Text