Um die aufgeworfene Frage zu beantworten, behandeln wir zunächst die Orthonormalität. Es soll also gelten:
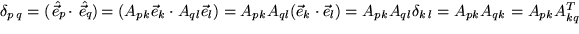
d.h.
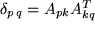
Wir können demnach nur Matrizen zulassen mit der Eigenschaft 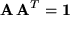 oder
oder 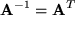 . Diese Matrizen heißen bei den Mathematikern orthogonal. Unter ihren neun Matrixelementen sind nur drei reelle Zahlen unabhängig wegen der sechs Bedingungsgleichungen:
. Diese Matrizen heißen bei den Mathematikern orthogonal. Unter ihren neun Matrixelementen sind nur drei reelle Zahlen unabhängig wegen der sechs Bedingungsgleichungen:
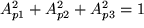 |
für 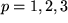 und und |
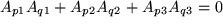 |
für 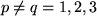 . . |
Die orthogonalen Matrizen bilden eine Gruppe, 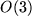 genannt, bezüglich der Multiplikation, die natürlich nicht abelsch sein kann, weil wir die Matrizenmultiplikation allgemein als nicht kommutativ gefunden haben:
genannt, bezüglich der Multiplikation, die natürlich nicht abelsch sein kann, weil wir die Matrizenmultiplikation allgemein als nicht kommutativ gefunden haben:
Um die Gruppeneigenschaft zu verifizieren, betrachten wir zunächst das Produkt  zweier orthogonaler Matrizen
zweier orthogonaler Matrizen 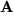 mit
mit 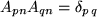 und
und 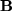 mit
mit 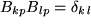 und berechnen:
und berechnen:
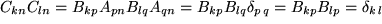
d.h. das Produkt zweier orthogonaler Matrizen ist wieder orthogonal.
Ferner gilt das Assoziative Gesetz wie für jede Matrizenmultiplikation:
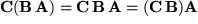
Es gibt genau ein Einselement, die Einheitsmatrix  ist nämlich orthogonal, da
ist nämlich orthogonal, da 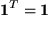 folgt
folgt 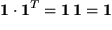 :
:
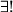 Einselement
Einselement 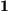 :
: 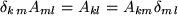 für alle
für alle 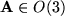
Denn die Multiplikation einer Matrix 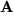 von links oder rechts mit der Einheitsmatrix
von links oder rechts mit der Einheitsmatrix 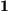 ergibt wieder die alte Matrix.
ergibt wieder die alte Matrix.
Und es existiert zu jeder orthogonalen Matrix 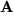 eine eindeutig bestimmte Inverse, nämlich genau die transponierte Matrix, das war ja gerade die Orthogonalitätsbedingung:
eine eindeutig bestimmte Inverse, nämlich genau die transponierte Matrix, das war ja gerade die Orthogonalitätsbedingung:
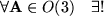
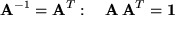
Die für die Existenz der Inversen notwendige Bedingung 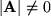 ist erfüllt, denn aus
ist erfüllt, denn aus 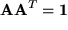 folgt für die Determinante
folgt für die Determinante
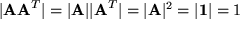
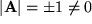
Damit sind alle Gruppeneigenschaften der othogonalen Matrizen bewiesen. Aus der Determinante sieht man darüber hinaus, dass es offenbar zwei Arten von orthogonalen Matrizen gibt, solche mit Determinante 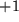 , die Drehungen, und andere mit Determinante
, die Drehungen, und andere mit Determinante 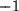 . Das sind gerade die Spiegelungen.
. Das sind gerade die Spiegelungen.
Die Definitionsgleichung für die orthogonalen Matrizen 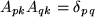 eröffnet noch einen ganz anderen Blick auf unser Kronecker-Symbol: Sobald wir nämlich links ein überflüssiges
eröffnet noch einen ganz anderen Blick auf unser Kronecker-Symbol: Sobald wir nämlich links ein überflüssiges 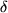 mit einer weiteren Summation hinzufügen, erhalten wir:
mit einer weiteren Summation hinzufügen, erhalten wir: 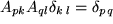 . Wenn wir das Kronecker-Symbol, seiner zwei Indizes wegen als Tensor zweiter Stufe ansehen, stehen auf der linken Seite
. Wenn wir das Kronecker-Symbol, seiner zwei Indizes wegen als Tensor zweiter Stufe ansehen, stehen auf der linken Seite  , d.h. die 9 Tensorkomponenten bezüglich des transformierten Koordinatensystems: jeweils eine Transformationsmatrix für jeden Index. Die ganze Gleichung
, d.h. die 9 Tensorkomponenten bezüglich des transformierten Koordinatensystems: jeweils eine Transformationsmatrix für jeden Index. Die ganze Gleichung 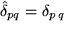 bedeutet dann die Invarianz der Matrixelemente gegenüber Drehungen und Spiegelungen, d.h. die Einsen und Nullen bleiben in jedem Koordinatensystem immer gleich und an derselben Stelle: Das gegenüber Vertauschen der Indizes symmetrische Kronecker-Symbol ist also, vom höheren Standpunkt betrachtet, ein "numerisch invarianter Tensor zweiter Stufe". Unter dieser Bezeichnung werden Sie ihm später auch häufig begegnen.
bedeutet dann die Invarianz der Matrixelemente gegenüber Drehungen und Spiegelungen, d.h. die Einsen und Nullen bleiben in jedem Koordinatensystem immer gleich und an derselben Stelle: Das gegenüber Vertauschen der Indizes symmetrische Kronecker-Symbol ist also, vom höheren Standpunkt betrachtet, ein "numerisch invarianter Tensor zweiter Stufe". Unter dieser Bezeichnung werden Sie ihm später auch häufig begegnen.