Zum Schluß dieses Kurses wollen wir nun noch überprüfen, wie sich unsere Produkte aus Vektoren unter Drehungen und Spiegelungen des Koordinatensystems verhalten:
Wir wissen schon, dass die Komponenten 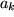 eines Vektors
eines Vektors 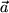 , der aus einer Verschiebung entstanden ist, als Projektionen auf die Koordinatenachsen
, der aus einer Verschiebung entstanden ist, als Projektionen auf die Koordinatenachsen 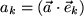 sich transformieren wie die Basisvektoren selbst:
sich transformieren wie die Basisvektoren selbst:
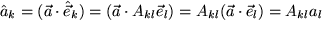
also
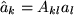 .
.
Insbesondere werden bei der Spiegelung am Nullpunkt, der Parität, die Vorzeichen umgedreht. Man nennt diese Vektoren deshalb polare Vektoren.
Als erstes Produkt untersuchen wir das Skalarprodukt 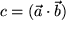 aus zwei polaren Vektoren
aus zwei polaren Vektoren 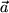 und
und 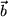 :
:
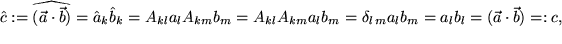 ,
,also
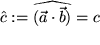 .
.
Wir haben dabei zuerst die Komponentendarstellung des Skalarprodukts im neuen System eingesetzt mit der Summe über 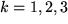 , dann das Transformationsgesetz für die Komponenten polarer Vektoren verwendet, die Orthogonalitätsrelation der Transformationsmatrizen ausgenützt und schließlich nach der Summation über
, dann das Transformationsgesetz für die Komponenten polarer Vektoren verwendet, die Orthogonalitätsrelation der Transformationsmatrizen ausgenützt und schließlich nach der Summation über 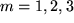 ohne irgend welche Vorfaktoren die Komponentendarstellung des Skalarprodukts im ursprünglichen Koordinatensystem erhalten.
ohne irgend welche Vorfaktoren die Komponentendarstellung des Skalarprodukts im ursprünglichen Koordinatensystem erhalten.
Damit haben wir gezeigt, dass unser Skalarprodukt dreh- und spiegelinvariant ist, also den Namen Skalar zurecht trägt.
Als nächstes studieren wir die Transformationseigenschaften der Komponenten 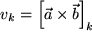 des Vektorprodukts
des Vektorprodukts 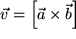 zweier polarer Vektoren
zweier polarer Vektoren 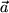 und
und 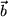 :
:
 ,
,also
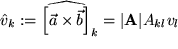 .
.
Dabei haben wir zunächst die Komponentendarstellung der k-ten Komponente des Vektorprodukts im transformierten Koordinatensystem mit Summationen über 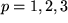 und
und 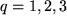 eingesetzt, dann die Transformation der Vektorkomponenten der beiden Faktoren durchgeführt und für den letzten Index des Levi-Civita-Symbols ein überflüssiges Kronecker-Symbol mit Summation über
eingesetzt, dann die Transformation der Vektorkomponenten der beiden Faktoren durchgeführt und für den letzten Index des Levi-Civita-Symbols ein überflüssiges Kronecker-Symbol mit Summation über 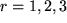 eingeführt. Dieses
eingeführt. Dieses 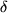 haben wir durch zwei orthogonale Transformationsmatrizen ersetzt und die drei Matrizen
haben wir durch zwei orthogonale Transformationsmatrizen ersetzt und die drei Matrizen 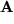 mit Hilfe unserer Determinanten-Formel
mit Hilfe unserer Determinanten-Formel 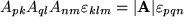 zur Determinante zusammengefaßt sowie das Vektorprodukt wieder im alten System geschrieben.
zur Determinante zusammengefaßt sowie das Vektorprodukt wieder im alten System geschrieben.
Daraus ergibt sich, dass das Vektorprodukt sich bei Drehungen zwar wie ein Verschiebungsvektor als Vektor transformiert, jedoch bei Spiegelungen wegen der Determinsnate 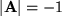 eine Vorzeichenänderung erfährt, also spiegelinvariant ist. Derartige Vektoren werden axiale Vektoren genannt und tatsächlich sind alle in der Physik auftretenden durch Vektorprodukte aus polaren Vektoren aufgebauten Vektoren spiegelungsinvariant. Sie hängen, wie wir gesehen haben alle mit Drehvorgängen zusammen und bedeuten im Gegensatz zum Richtungspfeil der Verschiebungsvektoren einen Drehsinn und der ändert sich, wie das folgende Bild zeigt, im Spiegel betrachtet nicht.
eine Vorzeichenänderung erfährt, also spiegelinvariant ist. Derartige Vektoren werden axiale Vektoren genannt und tatsächlich sind alle in der Physik auftretenden durch Vektorprodukte aus polaren Vektoren aufgebauten Vektoren spiegelungsinvariant. Sie hängen, wie wir gesehen haben alle mit Drehvorgängen zusammen und bedeuten im Gegensatz zum Richtungspfeil der Verschiebungsvektoren einen Drehsinn und der ändert sich, wie das folgende Bild zeigt, im Spiegel betrachtet nicht.
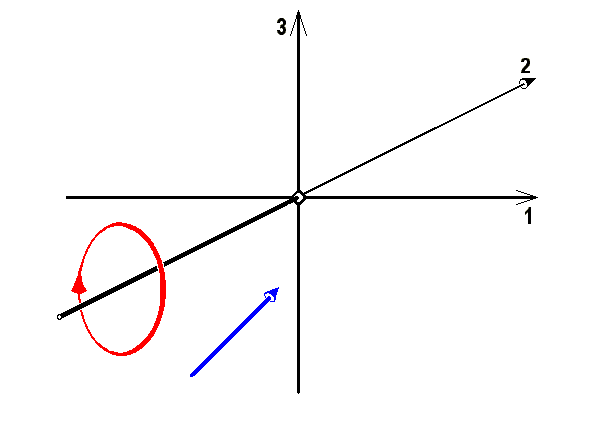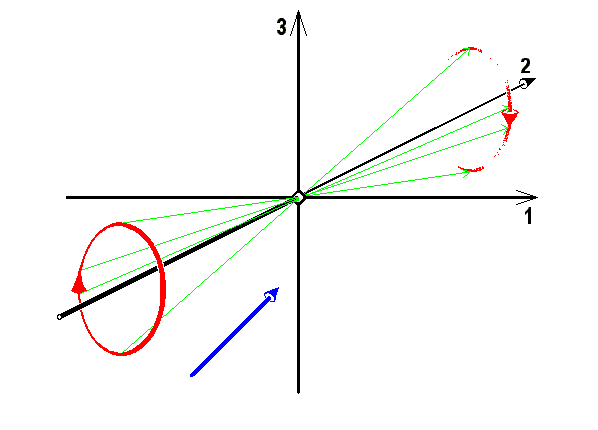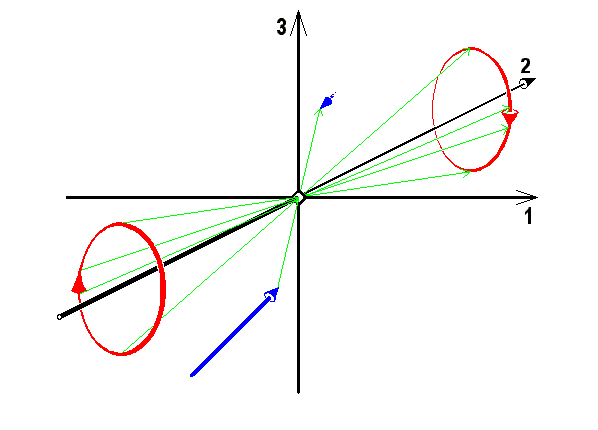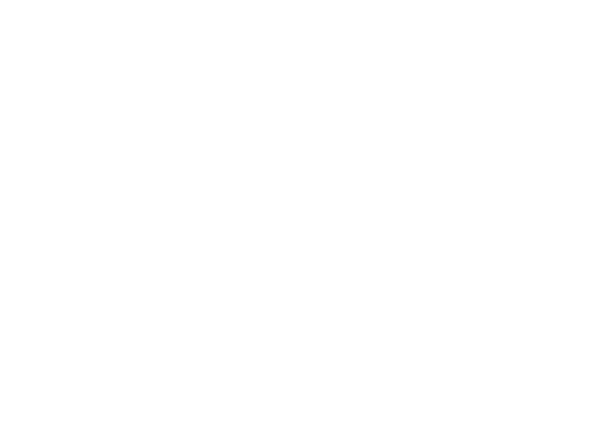
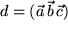 dreier polarer Vektoren
dreier polarer Vektoren 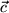 im transformierten Koordinatensystem
im transformierten Koordinatensystem 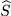 anschauen:
anschauen: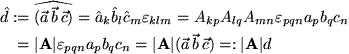 ,
,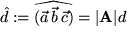 .
.
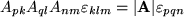 benützt.
benützt.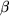 -Zerfall, z.B. in der Reaktion
-Zerfall, z.B. in der Reaktion 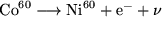 , das Spatprodukt der drei Impulse
, das Spatprodukt der drei Impulse 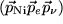 nicht verwenden?
nicht verwenden?