|
|
Forces and elasticity in cell adhesion
|
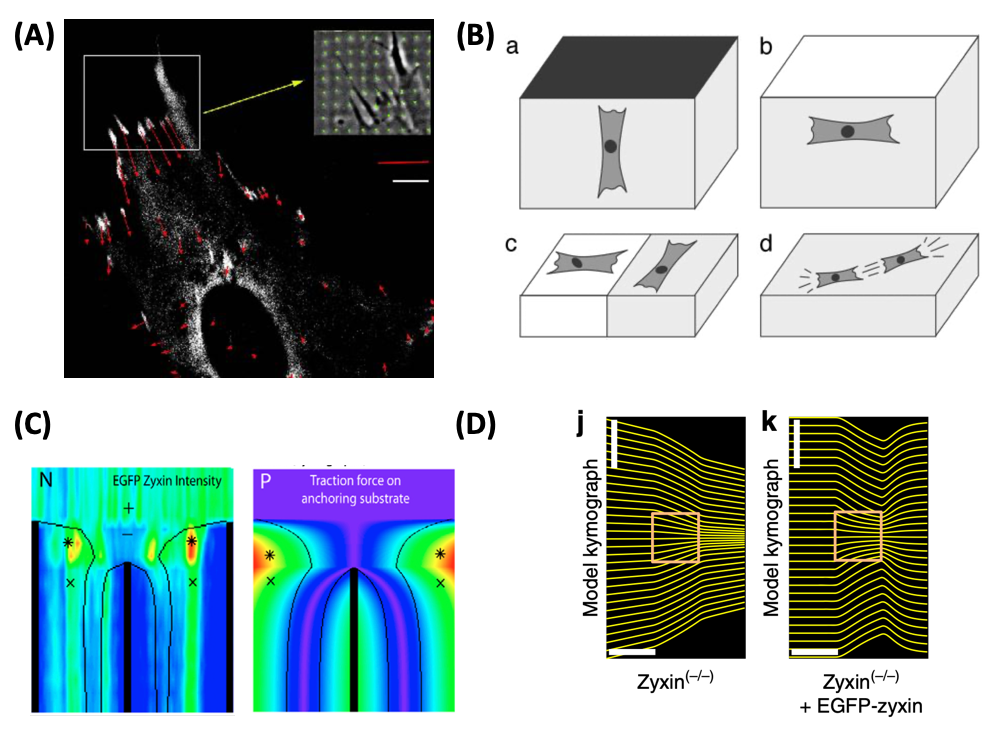
| Image: (A) Forces (red) exerted by an adhering fibroblast at sites of focal adhesions (white). The inset shows a phase contrast image of the deformation of the micro-patterned elastic substrate (green), from which the force pattern has been calculated (Balaban et al., Nature Cell Biology 2001). (B) Cells actively sense the elastic properties of their environment and strengthen contacts and cytoskeleton in the direction of large effective stiffness. Therefore they orient (a) perpendicular to clamped boundaries, (b) parallel to free boundaries, (c) perpendicular and parallel on the soft and stiff sides of a rigidity gradient, respectively, and (d) in parallel in and on a homogeneous medium (Bischofs and Schwarz, PNAS 2003). (C) Laser cutting of stress fibers reveals a close relation between forces and localization of the actin repair protein zyxin (Colombelli et al., Journal of Cell Science 2009). (D) Optogenetic activation of cell contractility shows that the same protein zyxin is required for cells to have elastic properties. Only when this protein is present does the cell build up internal elastic stress and backflow occurs when the activation period ends (Oakes et al., Nature Communications 2017). |
Force is ubiquitous in biological systems. Many essential cellular processes like cell division, cell adhesion and cell migration involve the generation of physical force. In most cases of interest, this force is generated internally by the actomyosin machinery and balanced either by the extracellular matrix or neighboring cells. For cell-matrix adhesion, the force therefore has to be funneled through so-called focal adhesion. Focal adhesions have both structural and signalling functions. From a mechanical point of view, they provide the pinning sites needed by the cell in order to spread out on the surface against its own elasticity; from a signalling point of view, focal adhesions signal successful adhesion to the cell. During my postdoctoral work at the Weizmann Institute, I became involved in a collaboration with experimentalists in the Department of Cell Biology which succeeded in measuring for the first time cellular forces at the level of focal adhesions (Balaban et al., Nature Cell Biology 2001, Biophysical Journal 2002). The experimental technique combined the use of microstructured elastic substrates and fluorescense marking of focal adhesions proteins. The theoretical part consisted in calculating the force pattern from the displacement pattern, which numerically amounts to solving an ill-posed inverse problem. We were able to show that size and direction of forces acting at focal adhesions correlate strongly with size and elongation of the adhesion plaques as monitored by GFP-vinculin (for fibroblasts, typical forces at focal adhesions are 10 nN, with a stress constant around 5.5 nN / micron^2). Thus force and protein assembly (which in turn correlates with signalling) are intimately linked at focal adhesions. In a related study, we were able to show that focal adhesions grow under the application of an external force (Riveline et al., J. Cell Biol. 2001).
Later we have improved the workflow required to measure cellular traction patterns. Our improvements in traction force microscopy include simultaneous use of several kinds of fluorescent markers, advances in image processing and filtering, and flexible use of different force reconstruction algorithms, eventually leading to a spatial resolution below micrometer (Sabass et al., Biophysical Journal 2008). We then applied this technique to correlate for the first time traction force with retrograde flow, which is a crucial element in cell migration and can be measured with speckle fluorescence microscopy. Combining it with traction force microscopy allowed us to identify a biphasic relation between flow and force (Gardel et al., Journal of Cell Biology 2008). In detail, we found that actin speed is inversely related to traction stress near the cell edge, indicating that the flow is increasingly impeded as the actin becomes increasingly engaged to the adhesions. In contrast, larger FAs where the actin speed is low are marked by a direct relationship between actin speed and traction stress. The crossover between these two regimes occurs at at threshold flow of around 10 nm/s, independent of many possible determinants like actin polymerization or myosin activity. Today actin retrograde flow is considered to be one of the first mechanosensitive processes during cell spreading (now often modeled with clutch models for sliding adhesion) and a prerequisite for the formation of mature focal adhesions, which are related to the generation of large forces and deformations. Although there has been some debate on how well the relation between force and size of focal adhesions holds for different cell types and different conditions (in particular for young versus old focal adhesions), there is no doubt that focal adhesions harbour a wealth of mechanosensitive processes and give a sense of touch to all cells.
One central question emerging from this experimental work is why cells can generate such high forces and keep them up for a long time given that they are build from soft material that typically flows under mechanical load. In a collaboration with Julien Colombelli and Ernst Stelzer from the EMBL at Heidelberg, who used laser cutting to probe the mechanics of stress fibers, we were able to show that cells use specific proteins like zyxin to reinforce their structure where high stresses are localized (Colombelli et al., Journal of Cell Science 2009). Using a theoretical model for stress distribution along stress fibers, we found that zyxin localization follows exactly the spatial distribution of force along the fiber. Therefore stress fibers act as spatially distributed mechanosensors. In a more recent collaboration with Patrick Oakes, Margaret Gardel and Michael Glotzer, who combined optogenetic activation of cell contractility with traction force microsopy, we found that the same protein zyxin is essential to keep stress fibers elastic, thus producing back flow after the activation has ended (Oakes et al. Nature Communications 2017). Together these results suggest that cells have evolved very specific mechanisms to achieve elasticity on supra-molecular scales. In some sense, this is similar to longevity genes that have evolved to repair the inevitable DNA-doublestrand breaks; because biological systems are hold together by weak interactions that allow them to be very dynamic in the first place, they need repair mechanisms to stay viable.
One important consequence arising from these experimental findings on force generation and mechanosensing by adherent cells is the possibility that cells might interact elasticity through the surrounding matrix. We have shown that a large body of experimental observations on cell organization in soft media can be consistently explained from a relatively simple theory which describes active cell behavior by an extremum principle in linear elasticity theory (PNAS 2003, Physical Review E 2004, Physical Review Letters 2005). Our theory uses concepts which have been developed in the 70s for elastic interactions of atomic defects in crystals. In detail, we model cells as anisotropic force contraction dipoles and solve the elastic equations for elastic isotropic material with different geometries and boundary conditions (Physical Review Letters 2002). We start from the observation that cells strengthen contacts and cytoskeleton in the direction of large effective stiffness in their environment (possibly because build-up of force at focal adhesions is more efficient in a stiff environment) and show that this corresponds to a minimization of the quantity W = uij Pij, where uij is the strain tensor of the surrounding medium (including image strain in the case of finitely sized geometries) and Pij is the force dipole tensor representing the cell. From this principle, we show that cells orient in the direction of one-time external tensile strain (for frequently recurrent perturbations, they tend to orientate themselves away in order to avoid mechanical disruption), that they orient parallel and normal to free and clamped surfaces, respectively, and that they interact elastically to form strings, in excellent agreement with experimental observations. Modelling cells as force dipoles is similar to the way one models microswimmers (e.g. bacteria like E. Coli or algae like Chlamydomonas) and has become a very powerful tool to investigate the interactions between cells and their elastic environments. While our initial calculations had been done with linear elasticity in order to arrive at an analytical theory, today it is clear that non-linear effects in the matrix are important to understand that these effects can propagate over very large distances.
To better understand the molecular processes underlying rigidity sensing, we used mathematical models to explore the coupling between mechanics and biochemistry. In a first very simple approach (two-spring model), we pointed out that due to the force balance between cell and matrix and because force is generated by molecular motors with a stall force, it is not so much the absolute value of stiffness that cells read out, but rather the relative extend by which they deform themselves versus the matrix, and how fast this build-up of force does occur (Schwarz et al., Biosystems 2006). Later we formulated very detailed mathematical models for the exact coupling between force generation and biochemistry in the Rho-pathway, and how this leads to positive feedbacks between stiff environments and force generation by myosin II molecular motors (Besser and Schwarz, New Journal of Physics 2007). Such insight is not only needed to understand optogenetic control of cell contractility (Oakes et al. Nature Communications 2017), but also many essential physiological processes, in particular cell division. For example, in a collaboration with the Lenart group, we recently were able to show that contraction waves in starfish oocytes are guided by the depletion of the cell cycle regulator Cdk1 after nuclear envelope breakdown (Bischof et al., Nature Communications 2017). In the long run, we aim at a quantitative understanding how force generation in cells is determined by the interplay of internal and external cues (e.g. progression in the cell cycle and extracellular matrix geometry), and how it feeds back to cellular decision making (e.g. during cancer cell migration or stem cell differentiation).
Reviews summarizing our work on cell forces and elasticity
- U. S. Schwarz and I. B. Bischofs. Physical determinants of cell organization in soft media. Med. Eng. Phys., 27:763-72, 2005. (abstract, doi:10.1016/j.medengphy.2005.04.007, PDF)
- U. S. Schwarz. Soft matters in cell adhesion: rigidity sensing on soft elastic substrates. Soft Matter 3: 263-266, 2007. (abstract, doi:10.1039/b606409d, PDF)
- Ulrich S. Schwarz and Margaret L. Gardel. United we stand - integrating the actin cytoskeleton and cell-matrix adhesions in cellular mechanotransduction. J. Cell Sci., 125:3051-3060, 2012. (DOI:10.1242/jcs.093716, PDF)
- Ulrich S. Schwarz and Samuel A. Safran. Physics of adherent cells. Rev. Mod. Phys., 85:1327-1381, Aug 2013. (abstract, journal website, arXiv:1309.2817, PDF)
Selected publications from collaborations with experimentalists
- N. Q. Balaban, U. S. Schwarz, D. Riveline, P. Goichberg, G. Tzur, I. Sabanay, D. Mahalu, S. Safran, A. Bershadsky, L. Addadi and B. Geiger, Force and focal adhesion assembly: a close relationship studied using elastic micro-patterned substrates, Nat. Cell Biol. 3: 466-472 (2001) (abstract, PDF)
- D. Riveline, E. Zamir, N. Q. Balaban, U. S. Schwarz, B. Geiger, Z. Kam, A. D. Bershadsky, Focal contact as a mechanosensor: externally applied local mechanical force induces growth of focal contacts by a mDia1-dependent and ROCK-independent mechanism, J. Cell Biol.153: 1175-1185 (2001) (abstract, PDF)
- U. S. Schwarz, N. Q. Balaban, D. Riveline, A. Bershadsky, B. Geiger, S. A. Safran, Calculation of forces at focal adhesions from elastic substrate data: the effect of localized force and the need for regularization, Biophys. J. 83: 1380-1394 (2002) (abstract, PDF)
- B. Sabass, M. L. Gardel, C. Waterman and U. S. Schwarz. High resolution traction force microscopy based on experimental and computational advances. Biophys. J., 94:207-220, 2008. (abstract, doi:10.1529/biophysj.107.113670, PDF)
- M. L. Gardel, B. Sabass, L. Ji, G. Danuser, U. S. Schwarz, and C. M. Waterman. Traction stress in focal adhesions correlates biphasically with actin retrograde flow speed. J. Cell Biol., 183:999-1005, 2008. (abstract, doi:10.1083/jcb.200810060, PDF)
- J. Colombelli, A. Besser, H. Kress, E.G. Reynaud, P. Girard, E. Caussinus, U. Haselmann, J.V. Small, U. S. Schwarz, and E.H.K. Stelzer. Mechanosensing in actin stress fibers revealed by a close correlation between force and protein localization. J. Cell Sci., 2009. (abstract, doi: 10.1242/jcs.042986, PDF)
- Patrick W. Oakes, Elizabeth Wagner, Christoph A. Brand, Dimitri Probst, Marco Linke, Ulrich S. Schwarz, Michael Glotzer, and Margaret L. Gardel. Optogenetic control of RhoA reveals zyxin-mediated elasticity of stress fibres. Nature Communications 8:15817, 2017. (journal website, PDF, BioRxiv)
- Johanna Bischof, Christoph A. Brand, Kalman Somogyi, Imre Majer, Sarah Thome, Masashi Mori, Ulrich S. Schwarz, and Peter Lenart. A Cdk1 gradient guides surface contraction waves in oocytes. Nature Communications, 8(1):849, October 2017. (journal website, PDF, PDF Erratum)
Selected theory work on cells in soft environments
- U. S. Schwarz and S. A. Safran, Elastic interactions of cells, Phys. Rev. Lett. 88: 048102 (2002) (abstract, cond-mat/0201110, PDF)
- I. B. Bischofs and U. S. Schwarz, Cell organization in soft media due to active mechanosensing, Proc. Natl. Acad. Sci. USA 100: 9274-9279 (2003) (abstract, cond-mat/0308187, PDF)
- I. B. Bischofs, S. A. Safran and U. S. Schwarz, Elastic interactions of active cells with soft materials, Phys. Rev. E 69: 021911 (2004) (abstract, cond-mat/0309427, DOI: 10.1103/PhysRevE.69.021911 PDF)
- U. S. Schwarz, T. Erdmann, and I. B. Bischofs. Focal adhesions as mechanosensors: the two-spring model. BioSystems, 83: 225-232 (2006) (abstract, q-bio.SC/0608006, PDF)
- A. Besser and U. S. Schwarz. Coupling biochemistry and mechanics in cell adhesion: a model for inhomogeneous stress fiber contraction. New J. Phys., 9:425, 2007. (abstract, qbio arXiv:0707.2551v2, doi:10.1088/1367-2630/9/11/425, PDF)
Last modified Mar 22 2020 by USS.
Back to home page Ulrich Schwarz.