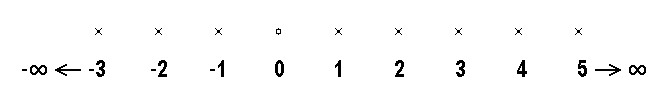Mit dem zivilisatorischen und kulturellen Fortschritt der Menschen mußten auch die Zahlen erweitert werden. Z.B. reicht es, wenn man von Geld spricht, nicht aus, den Betrag zu kennen (also die Zahl der Münzen), sondern man muß auch ausdrücken können, ob man sie besitzt oder schuldet. Das wird heute durch die Farbe der Zahl ( "rote Zahlen" ) oder durch ein Vorzeichen oder ausgedrückt. In den Naturwissenschaften haben sich die Vorzeichen eingebürgert.

Der Physiker kann eine Markierung auf seinem Maßstab um eine beliebige Zahl von Punkten nach rechts verschieben, stößt aber auf Schwierigkeiten beim Verschieben der Marke nach links. Mathematisch formuliert: Nicht für alle natürlichen Zahlen und hat die Gleichung eine Lösung , die auch eine natürliche Zahl ist: z.B. . Solche Gleichungen kann man nur dann lösen, wenn man die natürlichen Zahlen durch Hinzufügen der negativen Zahlen zu den ganzen Zahlen ergänzt:

Zu jedem positiven Element existiert dann genau ein

Auch zur kommt eine , d.h. ein Euro Schulden zu einem Euro Guthaben.

Die Mathematiker bezeichnen die Menge der ganzen Zahlen, die aus allen natürlichen Zahlen , aus ihren negativen Partnern und der Null bestehen, mit

Mit dieser Erweiterung hat die obige Gleichung wie gewünscht für alle Paare von ganzen Zahlen immer eine Lösung, nämlich die Differenz , die wieder eine ganze Zahl ist . Man sagt auch, sei "abgeschlossen" bezüglich der Addition: Die Addition führt nicht aus der Menge heraus. Dies bringt uns zu einem zentralen Begriff der Mathematik ( und auch der Physik ), dem der Gruppe:

Man bezeichnet eine Menge von Objekten ( wie z.B. die ganzen Zahlen ) als Gruppe, wenn

• sie abgeschlossen ist bezüglich einer inneren Verknüpfung ( wie z.B. der Addition ),
• ein Assoziatives Gesetz ( wie z.B.: 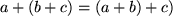) gilt,
• sie genau ein Neutrales Element ( wie z.B. die 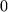) besitzt und
• zu jedem Element genau eine Umkehrung ( wie z.B. das Negative ) existiert.

Falls darüber hinaus auch noch das Kommutative Gesetz ( wie z.B. ) gilt, nennen die Mathematiker die Gruppe abelsch.

Die ganzen Zahlen kann man sich als äquidistante Punkte auf einer ganzen Geraden geometrisch vorstellen.