Nun folgt der Kernpunkt dieses ganzen Kapitels: Wie Sie aus der Projektion der Darstellungspunkte auf
die 2-Achse gesehen haben, gibt es Zahlenfolgen, deren Glieder
![]() sich auf der
Zahlengeraden um eine Zahl
sich auf der
Zahlengeraden um eine Zahl
![]() herum häufen,
so dass unendlich viele Folgenglieder, in jeder
herum häufen,
so dass unendlich viele Folgenglieder, in jeder
![]() -
Umgebung
-
Umgebung
![]() dieser Zahl
dieser Zahl
![]() liegen, die
übrigens nicht unbedingt selbst ein Glied der Folge zu sein braucht. Man nennt
liegen, die
übrigens nicht unbedingt selbst ein Glied der Folge zu sein braucht. Man nennt
![]() in einem solchen
Fall einen Häufungspunkt der Folge. Von unseren Beispielen hat die Folge der natürlichen
Zahlen (F1) keinen und die harmonische Folge (F3) einen Häufungspunkt, und zwar bei Null.
Die alternierende Folge (F2) hat sogar zwei Häufungspunkte: einen bei
in einem solchen
Fall einen Häufungspunkt der Folge. Von unseren Beispielen hat die Folge der natürlichen
Zahlen (F1) keinen und die harmonische Folge (F3) einen Häufungspunkt, und zwar bei Null.
Die alternierende Folge (F2) hat sogar zwei Häufungspunkte: einen bei
![]() und einen bei
und einen bei
![]() .
.
Der Satz von Bolzano und Weierstraß garantiert uns, dass jede nach oben und unten beschränkte Folge mindestens einen Häufungspunkt haben muß.
Falls eine Folge nur einen einzigen Häufungspunkt besitzt, kann es vorkommen, dass alle Folgenglieder ab einer bestimmten Nummer in der Umgebung dieses Punktes liegen. Man nennt diesen Punkt dann den Grenzwert der Folge und dieser Fall erweist sich als zentraler Begriff der Analysis: Die Mathematiker haben deshalb mehrere Bezeichnungen dafür. Sie sagen auch, die Folge hat einen Limes oder die Folge ist konvergent gegenMit dem letzten Stenogramm ist gemeint: für jede vorgegebene auch noch so kleine positive Zahl
![]() kann man eine
Nummer
kann man eine
Nummer ![]() angeben, so dass der Abstand vom Häufungspunkt
angeben, so dass der Abstand vom Häufungspunkt
![]() für alle
Folgenglieder mit einer größeren Nummer als
für alle
Folgenglieder mit einer größeren Nummer als
![]() kleiner ist
als das vorgegebene kleine
kleiner ist
als das vorgegebene kleine
![]() .
.
Für manche Folgen erkennt man die Konvergenz oder sogar den Grenzwert nach einiger Übung mit bloßem Auge, aber manchmal ist es gar nicht so einfach, festzustellen, ob eine Folge konvergent ist. Deshalb ist der Satz von Bolzano und Weierstraß sehr erwünscht, der uns zeigt, wann man ganz allgemein auf die Konvergenz einer Folge schließen kann:
|
Satz von Bolzano und Weierstraß: Jede nach oben beschränkte monoton steigende Folge ist konvergent, |
In all den Fällen, bei denen man den Grenzwert nicht kennt oder nicht leicht herausfinden kann,
hilft den Mathematikern oft auch das notwendige
![]() und
hinreichende
und
hinreichende
![]()
|
Cauchy - Kriterium:
|
d.h. eine Folge konvergiert genau dann, wenn die Abstände zwischen den Gliedern der Folge ab einer bestimmten Nummer immer kleiner werden, die entsprechenden Punkte auf der Zahlengeraden also immer näher zusammenrücken; wenn das nicht der Fall ist, dann divergiert sie.
Außerdem kann man zeigen, dass jede Teilfolge einer konvergenten Folge und die Summe und Differenz,
sowie das Produkt und, falls der Nenner ungleich
![]() ist,
auch der Quotient zweier konvergenten Folgen wieder konvergent sind, d.h. der Grenzwert ist mit den
rationalen Rechenoperationen vertauschbar.
ist,
auch der Quotient zweier konvergenten Folgen wieder konvergent sind, d.h. der Grenzwert ist mit den
rationalen Rechenoperationen vertauschbar.
Viele konvergente Folgen haben die Null als Häufungspunkt, man nennt sie Nullfolgen.
Die harmonische Folge (F3) mit
![]() ist z.B.
eine Nullfolge.
ist z.B.
eine Nullfolge.
Die Folgen (F1) und (F2) konvergieren offensichtlich nicht.
|
Aufgabe 3.4: Konvergente Folgen
|
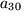 .
.