Die Bildung des Grenzwerts für Funktionen wird durch folgende Überlegung auf die uns bereits bekannte Berechnung von Grenzwerten von Folgen zurückgeführt:
Wenn wir wissen wollen, ob die Funktionswerte  einer reellen Funktion
einer reellen Funktion 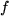 bei Annäherung des Arguments
bei Annäherung des Arguments  an eine reelle Zahl
an eine reelle Zahl  die Zahl
die Zahl 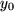 als Grenzwert hat, wählen wir eine Folge
als Grenzwert hat, wählen wir eine Folge 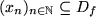 von reellen Zahlen im Definitionsbereich
von reellen Zahlen im Definitionsbereich 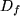 der Funktion
der Funktion 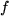 , die für
, die für 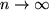 gegen die Zahl
gegen die Zahl 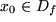 strebt. Dann bilden wir die Funktionswerte an diesen Stellen
strebt. Dann bilden wir die Funktionswerte an diesen Stellen 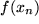 , die wieder eine Folge darstellen
, die wieder eine Folge darstellen 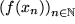 , und überprüfen, ob diese Folge der Funktionswerte gegen
, und überprüfen, ob diese Folge der Funktionswerte gegen 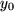 konvergiert. Falls sich das für jede aus dem Definitionsbereich herausgegriffene gegen
konvergiert. Falls sich das für jede aus dem Definitionsbereich herausgegriffene gegen  strebende Folge zeigen läßt, dann nennen wir die Folge der Funktionswerte konvergent gegen
strebende Folge zeigen läßt, dann nennen wir die Folge der Funktionswerte konvergent gegen 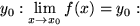
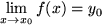 konvergent:
konvergent: 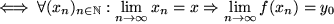
Wenn wir unsere Definition der Konvergenz für Folgen einsetzen, ergibt das:
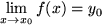 konvergent:
konvergent: 
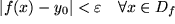 mit
mit 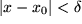
Dies für alle Folgen zu zeigen, ist natürlich leichter gesagt als getan! Wir brauchen uns hier jedoch nicht zu lange mit diesen zum Teil schwierigen mathematischen Fragen zu beschäftigen, mit denen Sie sich in der Analysis-Vorlesung noch auseinanderzusetzen Gelegenheit haben werden, sondern wollen uns mit einigen für die Physiker wichtigen Beispielen begnügen.
Bereits aus den Graphen sieht man z.B.
für das Verhalten am Ursprung, dass bei den Potenzen 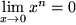 ist und
ist und 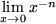 divergent für
divergent für  . Außerdem sieht man leicht, dass
. Außerdem sieht man leicht, dass 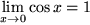 und
und 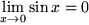 .
.
Für das Verhalten bei großen Werten der Variablen ist 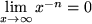 und
und 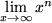 divergiert. Auch ist
divergiert. Auch ist 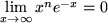 und
und 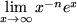 divergiert. Man sagt deshalb, dass die Exponentialfunktion stärker ansteigt als jede Potenzfunktion.
divergiert. Man sagt deshalb, dass die Exponentialfunktion stärker ansteigt als jede Potenzfunktion.
|
Aufgabe 4.14: Grenzwerte von Funktionen Berechnen Sie a) b) c) d) Untersuchen Sie mit Hilfe der Umkehrfunktion und der Exponentialfolge folgenden Grenzwert |
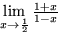
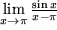
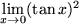
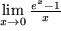 , den wir im nächsten Kapitel benützen und im übernächsten Kapitel auf viel elegantere Weise erneut ableiten werden.
, den wir im nächsten Kapitel benützen und im übernächsten Kapitel auf viel elegantere Weise erneut ableiten werden.