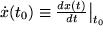Der Differenzenquotient 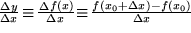 ist bei diesem Grenzübergang
ist bei diesem Grenzübergang 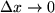 in den sogenannten Differentialquotienten übergegangen, von seinem Erfinder Leibniz mit
in den sogenannten Differentialquotienten übergegangen, von seinem Erfinder Leibniz mit 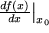 oder
oder 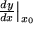 bezeichnet, jedoch zunächst eigentlich selbst kein Quotient, sondern nur der Grenzwert eines Quotienten. Wie bei allen fundamentalen Begriffen der Mathematik gibt es auch hier wieder mehrere Bezeichnungen: Die alternative, den meisten von der Schule her geläufige Bezeichnung
bezeichnet, jedoch zunächst eigentlich selbst kein Quotient, sondern nur der Grenzwert eines Quotienten. Wie bei allen fundamentalen Begriffen der Mathematik gibt es auch hier wieder mehrere Bezeichnungen: Die alternative, den meisten von der Schule her geläufige Bezeichnung 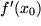 , gesprochen "f Strich an der Stelle
, gesprochen "f Strich an der Stelle  ", stammt von Lagrange und soll daran erinnern, dass die Steigung des Graphen, auch (erste) Ableitung der Funktion genannt, im allgemeinen selbst wieder eine neue, entlang der Kurve variierende Funktion der unabhängigen Variablen
", stammt von Lagrange und soll daran erinnern, dass die Steigung des Graphen, auch (erste) Ableitung der Funktion genannt, im allgemeinen selbst wieder eine neue, entlang der Kurve variierende Funktion der unabhängigen Variablen  ist, hier speziell an der Stelle
ist, hier speziell an der Stelle  angegeben. Auch die Bezeichnung
angegeben. Auch die Bezeichnung 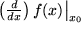 ist im Gebrauch, die betont, dass die Differentiation eine "Operation" ist, bei der der "Differentialoperator"
ist im Gebrauch, die betont, dass die Differentiation eine "Operation" ist, bei der der "Differentialoperator" 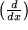 auf die rechts stehende Funktion
auf die rechts stehende Funktion  wirkt und das Resultat dann speziell an der Stelle
wirkt und das Resultat dann speziell an der Stelle 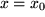 genommen werden soll. Es ist sinnvoll, alle diese Bezeichnungen nebeneinander zur Verfügung zu haben je nach dem Aspekt, auf den es gerade ankommt.
genommen werden soll. Es ist sinnvoll, alle diese Bezeichnungen nebeneinander zur Verfügung zu haben je nach dem Aspekt, auf den es gerade ankommt.
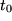 wählen wir demnach einen beliebigen Zeitpunkt
wählen wir demnach einen beliebigen Zeitpunkt 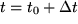 in der Nähe von
in der Nähe von 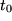 und zeichnen die Sekante durch die Funktionswerte
und zeichnen die Sekante durch die Funktionswerte 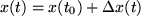 und
und 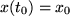 , bestimmen deren Steigung als Differenzenquotient:
, bestimmen deren Steigung als Differenzenquotient: 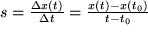 und lassen dann den Zeitpunkt
und lassen dann den Zeitpunkt 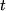 gegen
gegen 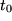 , also
, also 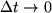 gehen. Dabei nähert sich bei einer stetigen Funktion auch
gehen. Dabei nähert sich bei einer stetigen Funktion auch 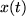 dem Wert
dem Wert 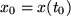 und die Sekante geht in die Tangente des Graphs über mit der
und die Sekante geht in die Tangente des Graphs über mit der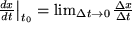
 für die unabhängige und
für die unabhängige und 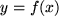 für die abhängige Variable ergibt sich so der :
für die abhängige Variable ergibt sich so der :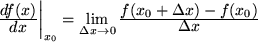
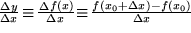 ist bei diesem Grenzübergang
ist bei diesem Grenzübergang 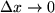 in den sogenannten Differentialquotienten übergegangen, von seinem Erfinder Leibniz mit
in den sogenannten Differentialquotienten übergegangen, von seinem Erfinder Leibniz mit 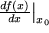 oder
oder 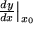 bezeichnet, jedoch zunächst eigentlich selbst kein Quotient, sondern nur der Grenzwert eines Quotienten. Wie bei allen fundamentalen Begriffen der Mathematik gibt es auch hier wieder mehrere Bezeichnungen: Die alternative, den meisten von der Schule her geläufige Bezeichnung
bezeichnet, jedoch zunächst eigentlich selbst kein Quotient, sondern nur der Grenzwert eines Quotienten. Wie bei allen fundamentalen Begriffen der Mathematik gibt es auch hier wieder mehrere Bezeichnungen: Die alternative, den meisten von der Schule her geläufige Bezeichnung 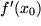 , gesprochen "f Strich an der Stelle
, gesprochen "f Strich an der Stelle  ", stammt von Lagrange und soll daran erinnern, dass die Steigung des Graphen, auch (erste) Ableitung der Funktion genannt, im allgemeinen selbst wieder eine neue, entlang der Kurve variierende Funktion der unabhängigen Variablen
", stammt von Lagrange und soll daran erinnern, dass die Steigung des Graphen, auch (erste) Ableitung der Funktion genannt, im allgemeinen selbst wieder eine neue, entlang der Kurve variierende Funktion der unabhängigen Variablen 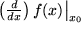 ist im Gebrauch, die betont, dass die Differentiation eine "Operation" ist, bei der der "Differentialoperator"
ist im Gebrauch, die betont, dass die Differentiation eine "Operation" ist, bei der der "Differentialoperator" 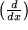 auf die rechts stehende Funktion
auf die rechts stehende Funktion  wirkt und das Resultat dann speziell an der Stelle
wirkt und das Resultat dann speziell an der Stelle 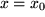 genommen werden soll. Es ist sinnvoll, alle diese Bezeichnungen nebeneinander zur Verfügung zu haben je nach dem Aspekt, auf den es gerade ankommt.
genommen werden soll. Es ist sinnvoll, alle diese Bezeichnungen nebeneinander zur Verfügung zu haben je nach dem Aspekt, auf den es gerade ankommt.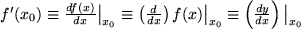
 "Strich" einen hochgesetzten
"Strich" einen hochgesetzten  "Punkt":
"Punkt":