Der Differentialquotient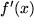 
einer Funktion 
ist selbst wieder eine Funktion der unabhängigen Variablen 
. Ist sie wieder differenzierbar, kommen wir vom Differentialquotienten, der "ersten Ableitung" oder Steigung einer Funktion, zur
Der Differentialquotient 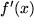einer Funktion ist selbst wieder eine Funktion der unabhängigen Variablen . Ist sie wieder differenzierbar, kommen wir vom Differentialquotienten, der "ersten Ableitung" oder Steigung einer Funktion, zur
zweiten Ableitung: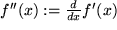 
, d.h.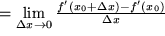 
Wieder gibt es verschiedene Schreibweisen: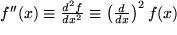 
. Die geometrische Bedeutung der zweiten Ableitung als Krümmung ergibt sich daraus, dass das Anwachsen der Steigung, d.h. eine positive zweite Ableitung 
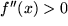( in positiver Richtung der unabhängigen Variablen betrachtet ) eine Linkskurve bedeutet, ein negatives 
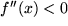entsprechend eine Rechtkurve. Wenn 
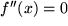, erkennt man, dass eine Gerade ist.
Für die Physiker erhalten wir, falls die Zeit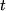 
als unabhängige Variable auftritt, Altbekanntes, nämlich die Beschleunigung als erste zeitliche Ableitung der Geschwindigkeit oder zweite zeitliche Ableitung des Ortes: 
.
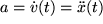Sukzessiv erhalten wir für viele Funktionen auch noch höhere Ableitungen, allgemein etwa die
n-te Ableitung: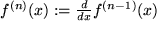
mit 
.
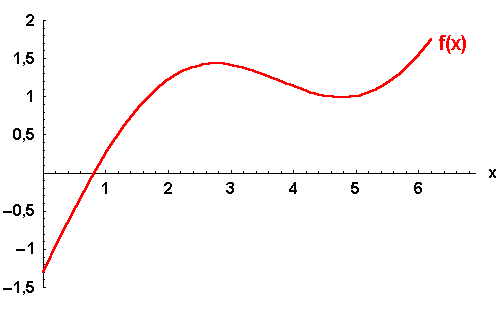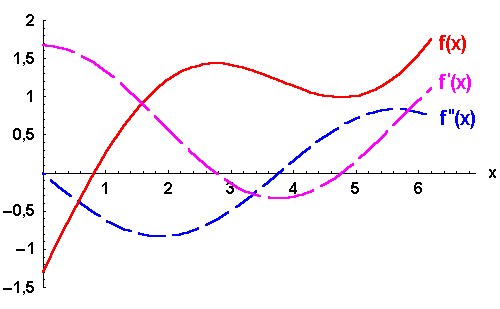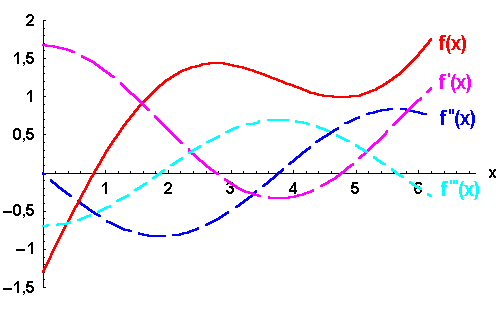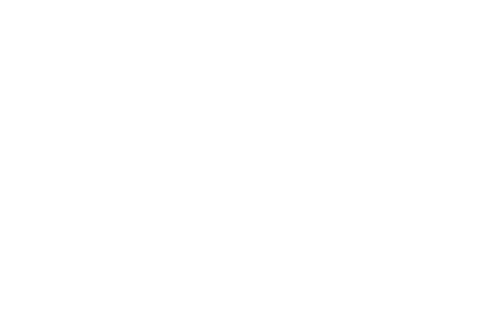
Bild 5.4: Graph einer Funktion und ihrer höheren Ableitungen