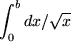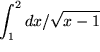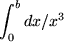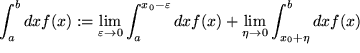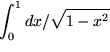7 Integration

7.6 Uneigentliche Integrale

7.6.2 Unbeschränkter Integrand

Nun werfen wir einen kurzen Blick auf den zweiten Fall, wenn nämlich der Integrand an einer Stelle des endlichen Integrationsintervalls unbeschränkt ist, z.B. an der unteren Grenze: . Wir berechnen dazu das Integral von einem Wert ab, der nur eine kleine Strecke oberhalb der kritischen Stelle liegt und lassen erst im Ergebnis der Integration diese kleine Strecke gegen Null gehen. Falls dieser Grenzwert dann existiert, nennen wir ihn ein uneigentliches Integral der zweiten Art und schreiben:

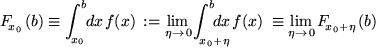
Als Beispiel berechnen wir für und ein kleines positives :

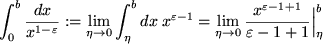
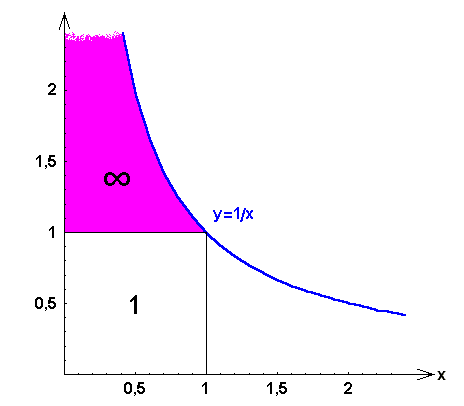
Wir sehen daraus, dass das uneigentliche Integral existiert, wenn die Funktion für kleiner werdende auch nur ein klein wenig schwächer ansteigt als , also z.B. für , dass aber für die im folgenden Bild

Bild 7.13

farbige Fläche unter der Funktion , genau das an der Winkelhalbierenden gespiegelte Bild der früher betrachteten Fläche, gerade keinen endlichen Flächeninhalt mehr besitzt und ebenso für alle stärker ansteigenden Funktionen wie etwa .

Wieder verfahren wir ganz analog bei einer Funktion, die an der oberen Grenze unbeschränkt wird:

oder, falls die Funktion an einer Stelle mitten im Integrationsintervall unbeschränkt ist:

Mit Integralen, die uneigentlich sowohl erster als auch zweiter Art sind wollen wir uns hier nicht befassen, obwohl auch diese durch säuberlich getrennte Grenzübergänge gemeistert werden können.

Sie werden später insbesondere bei den Funktionen mehrerer Variabler noch eine Vielfalt von weiteren Integralen kennen lernen: Kurven- oder Linien-Integrale, Oberflächen- und Volumen-Integrale in Räumen verschiedener Dimension. Wenn es jedoch darum geht, Zahlen auszurechnen, um mit Meßwerten zu vergleichen, werden Sie nichts anderes tun, als Riemann-Integrale berechnen, wie wir das hier zusammen erarbeitet haben.