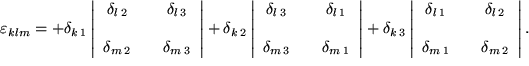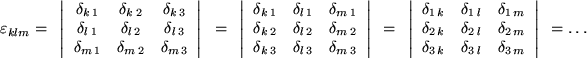Wir schreiben einfach:
Rechtssysem:
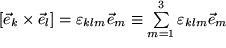
wobei der letzte Term noch einmal an die Einsteinsche Summenkonvention erinnert.
Dabei ist das Levi-Civita-Symbol mit seinen drei Indizes definiert durch:
|
Levi-Civita-Symbol

|
Das Symbol ändert offenbar das Vorzeichen beim Vertauschen je zweier Indizes, man nennt das total
antisymmetrisch gegen Vertauschen der Indizes:
Totale Antisymmetrie:
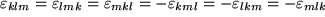
Bei allen geraden oder zyklischen Permutationen der
Zahlenfolge 123 in den Indizes ergibt der Wert
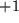 genau die drei oben angegebenen eine Rechtsbasis charakterisierenden Relationen.
Die Indexkonstellationen mit einer ungeraden Zahl von Vertauschungen je zweier Indizes bzw.
antizyklischen Permutationen von 123 führen auf die
genau die drei oben angegebenen eine Rechtsbasis charakterisierenden Relationen.
Die Indexkonstellationen mit einer ungeraden Zahl von Vertauschungen je zweier Indizes bzw.
antizyklischen Permutationen von 123 führen auf die
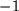 in den drei oben ebenfalls aufgeführten Vektorprodukten mit vertauschter Reihenfolge der Faktoren.
Nur sechs der 27 Elemente des Symbols sind verschieden von
in den drei oben ebenfalls aufgeführten Vektorprodukten mit vertauschter Reihenfolge der Faktoren.
Nur sechs der 27 Elemente des Symbols sind verschieden von
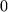 .
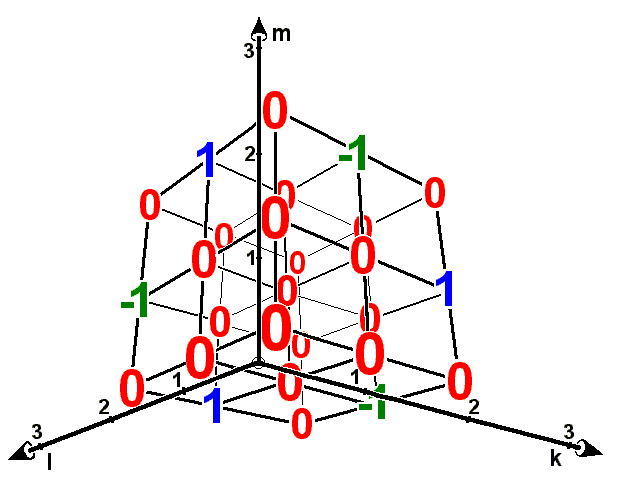
Alle 21 übrigen Elemente sind Nullen, so dass Sie Mühe haben, im folgenden Bild vor lauter
Nullen die vom Ursprung aus gesehen bemerkenswert symmetrisch angeordneten wichtigen drei blauen
Einsen und vor allem die noch wichtigeren grünen
.
Alle 21 übrigen Elemente sind Nullen, so dass Sie Mühe haben, im folgenden Bild vor lauter
Nullen die vom Ursprung aus gesehen bemerkenswert symmetrisch angeordneten wichtigen drei blauen
Einsen und vor allem die noch wichtigeren grünen
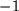 zu finden:
zu finden:
Wie Sie aus dem Bild sehen, ist das Levi-Civita-Symbol trotz der vielen Nullen und seiner schönen
Symmetrie wegen seiner drei Indizes ein ziemlich unhandliches Objekt.
Deshalb wollen wir seine entscheidende Botschaft, nämlich die sechs Indexkonfigurationen,
bei denen es nicht verschwindet, allein mit den uns schon vertrauteren handlichen
Kronecker-Symbolen formulieren, es ist nämlich
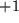 bei
bei
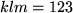 ,
,
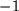 bei
bei
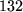 ;
;
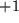 bei
bei
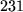 ,
,
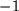 bei
bei
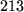 ;
;
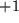 bei
bei
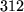 und
und
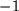 bei
bei
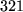 :
:
In dieser Form des Ergebnisses erkennen wir (nach unserer Schublade über das Rechnen mit
Matrizen) die Entwicklung der
Determinante einer
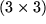 -Matrix
nach der ersten Zeile oder der ersten Spalte:
-Matrix
nach der ersten Zeile oder der ersten Spalte:
Also:
Beim Übergang von der ersten zur zweiten Version wurde berücksichtigt, dass die Determinante einer Matrix
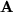 sich bei der Spiegelung an der Hauptdiagonalen nicht ändert:
sich bei der Spiegelung an der Hauptdiagonalen nicht ändert:
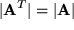 .
Beim Übergang zur dritten Version haben wir die Symmetrie des Kronecker-Symbols gegen Vertauschen der
beiden Indizes ausgenützt:
.
Beim Übergang zur dritten Version haben wir die Symmetrie des Kronecker-Symbols gegen Vertauschen der
beiden Indizes ausgenützt:
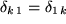 .
Es gibt offensichtlich noch eine Fülle von weiteren Formen des Levi-Civita-Symbols als Determinante,
wenn wir etwa berücksichtigen, dass jede Determinante beim Vertauschen zweier Zeilen oder Spalten ihr
Vorzeichen ändert. Bei der Determinantendarstellung des Levi-Civita-Symbols sollten Sie sich immer
daran erinnern, dass die Kronecker-Symbole in der Determinante nichts anderes sind als Platzhalter,
die je nach dem Wert der Indizes lediglich sagen, ob da eine
.
Es gibt offensichtlich noch eine Fülle von weiteren Formen des Levi-Civita-Symbols als Determinante,
wenn wir etwa berücksichtigen, dass jede Determinante beim Vertauschen zweier Zeilen oder Spalten ihr
Vorzeichen ändert. Bei der Determinantendarstellung des Levi-Civita-Symbols sollten Sie sich immer
daran erinnern, dass die Kronecker-Symbole in der Determinante nichts anderes sind als Platzhalter,
die je nach dem Wert der Indizes lediglich sagen, ob da eine
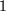 oder eine
oder eine
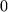 steht.
steht.
|
Aufgabe 9.36: Normalenvektoren
Welche Einheitsvektoren stehen senkrecht auf:
|
|
Aufgabe 9.37: Tetraederoberfläche:
Berechnen Sie die Oberfläche eines Tetraeders der Kantenlänge
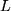 mit Hilfe der Vektorprodukte, indem Sie ihn in einen Würfel der Kantenlänge
mit Hilfe der Vektorprodukte, indem Sie ihn in einen Würfel der Kantenlänge
 einbetten.
Lösung einbetten.
Lösung
|
![]() genau die drei oben angegebenen eine Rechtsbasis charakterisierenden Relationen.
Die Indexkonstellationen mit einer ungeraden Zahl von Vertauschungen je zweier Indizes bzw.
antizyklischen Permutationen von 123 führen auf die
genau die drei oben angegebenen eine Rechtsbasis charakterisierenden Relationen.
Die Indexkonstellationen mit einer ungeraden Zahl von Vertauschungen je zweier Indizes bzw.
antizyklischen Permutationen von 123 führen auf die
![]() in den drei oben ebenfalls aufgeführten Vektorprodukten mit vertauschter Reihenfolge der Faktoren.
Nur sechs der 27 Elemente des Symbols sind verschieden von
in den drei oben ebenfalls aufgeführten Vektorprodukten mit vertauschter Reihenfolge der Faktoren.
Nur sechs der 27 Elemente des Symbols sind verschieden von
![]() .
Alle 21 übrigen Elemente sind Nullen, so dass Sie Mühe haben, im folgenden Bild vor lauter
Nullen die vom Ursprung aus gesehen bemerkenswert symmetrisch angeordneten wichtigen drei blauen
Einsen und vor allem die noch wichtigeren grünen
.
Alle 21 übrigen Elemente sind Nullen, so dass Sie Mühe haben, im folgenden Bild vor lauter
Nullen die vom Ursprung aus gesehen bemerkenswert symmetrisch angeordneten wichtigen drei blauen
Einsen und vor allem die noch wichtigeren grünen
![]() zu finden:
zu finden: