Die einfachste und wichtigste Art, drei Vektoren
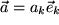 ,
,
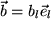 und
und
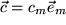 (jeweils mit Summenkonvention!) miteinander zu multiplizieren ist das Skalarprodukt eines Vektorprodukts mit einem dritten Vektor, das sogenannte
(jeweils mit Summenkonvention!) miteinander zu multiplizieren ist das Skalarprodukt eines Vektorprodukts mit einem dritten Vektor, das sogenannte
|
Spatprodukt:
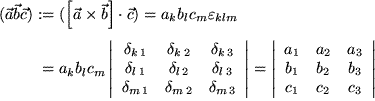
|
Dabei haben wir zunächst die Definitionen der beiden Produkte hingeschrieben, dann die Determinantendarstellung für das Levi-Civita-Symbol eingesetzt und vor der Ausführung der drei Summationen verwendet, dass die Determinante, wie wir früher gelernt haben, reihenweise homogen ist. Entsprechend den Umformungsmöglichkeiten der Determinanten sind weitere Formulierungen möglich, insbesondere durch zyklische Permutation und Spiegelung an der Hauptdiagonalen, d.h. die Komponenten der drei Vektoren können statt in die Zeilen auch in die Spalten der Determinante eingetragen werden.
Dieser Vielfalt der Möglichkeiten bei der Formulierung der Determinanten entsprechen viele Identitäten in den Darstellungen ein und desselben Spatprodukts in der konventionellen Form:
Wegen des Kommutativgesetzes des Skalarprodukts können darüber hinaus die beiden Malzeichen vertauscht und deshalb überhaupt weggelassen werden:
Die Antikommutativität des Vektorprodukts führt zu folgenden Relationen:
Die Auswertung der Determinante ergibt eine reelle Zahl:
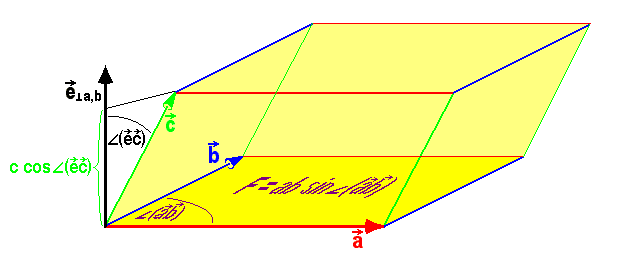
Zur geometrischen Deutung, betrachten wir die nächste Abbildung:
Das Vektorprodukt
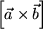 ergibt einen Vektor mit einer Länge von der Größe der Parallelogrammfläche
ergibt einen Vektor mit einer Länge von der Größe der Parallelogrammfläche
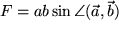 und der Richtung von
und der Richtung von
 , also senkrecht auf dem von
, also senkrecht auf dem von
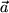 und
und
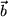 aufgespannten Parallelogramm. Auf die Richtung dieses Einheitsvektors
aufgespannten Parallelogramm. Auf die Richtung dieses Einheitsvektors
 wird nun der dritte Vektor
wird nun der dritte Vektor
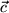 projiziert. Die Länge dieser Projektion
projiziert. Die Länge dieser Projektion
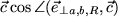 ergibt die Höhe eines Spats (: Parallelepipeds) über der Grundfläche
ergibt die Höhe eines Spats (: Parallelepipeds) über der Grundfläche
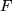 , dessen Volumeninhalt (allerdings mit Vorzeichen!) den Zahlenwert des Spatprodukts bedeutet. Je nach der Numerierung der drei Vektoren ist der Volumeninhalt mit einem Vorzeichen zu versehen.
, dessen Volumeninhalt (allerdings mit Vorzeichen!) den Zahlenwert des Spatprodukts bedeutet. Je nach der Numerierung der drei Vektoren ist der Volumeninhalt mit einem Vorzeichen zu versehen.
Falls beide Winkel kleiner als
 sind und die Vektoren in der angegebenen Reihenfolge eine Rechtsschraube bilden, ist der Volumeninhalt positiv zu nehmen. Betrachten Sie zum Beispiel den ersten Einheitsvektor
sind und die Vektoren in der angegebenen Reihenfolge eine Rechtsschraube bilden, ist der Volumeninhalt positiv zu nehmen. Betrachten Sie zum Beispiel den ersten Einheitsvektor
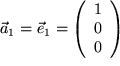 , den Einheitsvektor
, den Einheitsvektor
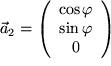 in der 1-2-Ebene, der mit
in der 1-2-Ebene, der mit
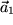 den Winkel
den Winkel
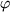 bildet, und den Vektor
bildet, und den Vektor
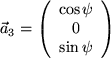 , der in der 1-3-Ebene mit
, der in der 1-3-Ebene mit
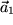 den Winkel
den Winkel
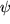 einschließt, so wird das Spatprodukt
einschließt, so wird das Spatprodukt
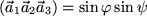 etwa gleich
etwa gleich
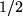 für
für
 und
und
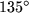 , während
, während
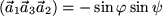 .
.
Der Volumeninhalt ist gleich
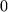 , wenn die drei Faktorvektoren komplanar, also linear abhängig sind, insbesondere wenn zwei der drei Faktoren gleich sind. Umgekehrt kann man vom Verschwinden der Determinante mit drei Vektoren als Zeilen- oder Spaltenvektoren auf deren lineare Abhängigkeit schließen.
, wenn die drei Faktorvektoren komplanar, also linear abhängig sind, insbesondere wenn zwei der drei Faktoren gleich sind. Umgekehrt kann man vom Verschwinden der Determinante mit drei Vektoren als Zeilen- oder Spaltenvektoren auf deren lineare Abhängigkeit schließen.
|
Aufgabe 9.39: Lineare Abhängigkeit
Sind die Vektoren
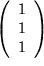 , ,
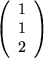 und und
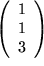 linear unabhängig? Lösung linear unabhängig? Lösung
|
Speziell für die Basisvektoren erhalten wir eine äußerst prägnante Formulierung für die Orthonormalität und Kennzeichnung eines Rechtssystems in einer einzigen Gleichung, die andererseits auch das Levi-Civita-Symbol durch die Basisvektoren darstellt:
Speziell gilt
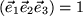 , der Volumeninhalt des Einheitswürfels.
, der Volumeninhalt des Einheitswürfels.
|
Aufgabe 9.40: Spatprodukt
Berechnen Sie folgende Spatprodukte:
|
|
Aufgabe 9.42:
| a) |
Drücken Sie das Levi-Civita-Symbol durch Kronecker-Symbole aus. Lösung |
| b) |
Drücken Sie das Kronecker-Symbol durch Levi-Civita-Symbole aus. Lösung |
| c) |
Drücken Sie das Levi-Civita-Symbol durch die Einheitsvektoren aus. Lösung |
| d) |
Drücken Sie das Kronecker-Symbol durch die Einheitsvektoren aus. Lösung |
|
![]() ,
,
![]() und
und
![]() (jeweils mit Summenkonvention!) miteinander zu multiplizieren ist das Skalarprodukt eines Vektorprodukts mit einem dritten Vektor, das sogenannte
(jeweils mit Summenkonvention!) miteinander zu multiplizieren ist das Skalarprodukt eines Vektorprodukts mit einem dritten Vektor, das sogenannte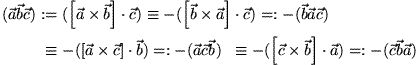
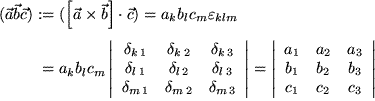
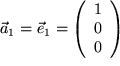 , den Einheitsvektor
, den Einheitsvektor
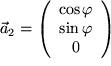 in der 1-2-Ebene, der mit
in der 1-2-Ebene, der mit
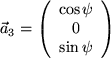 , der in der 1-3-Ebene mit
, der in der 1-3-Ebene mit