Three and more Problems - One Solution
Floating Bodies of Equilibrium in two dimensions,
the Tire Track Problem and
Electrons in a Parabolic Magnetic Field
Deutsch
Franz Wegner
Institut für Theoretische Physik
Ruprecht-Karls-Universität Heidelberg
The purpose of this paper is twofold:
After stating the three problems considered in the
paper
physics/0701241 (where also references can be found)
(i) the solution is described, where nearly no use of
mathematics is required, and
(ii) animations to some of these solutions are
shown.
Some mathematical formulae and supplements are given in
ps-file and pdf-file,
resp.
However, we report shortly that more problems are solved by the solutions, before we go through this program.
Solution of more problems
G. Bor, M. Levi, R. Perline, and S. Tabachnikov found in their paper "The
track geometry and integrable curve evolution"
arXiv: 1705.06314
(2017) that the curves,
which solve the three problems are solutions of several other problems.
The linear limit described below yields the shape of
the Elastica calculated by James Bernoulli in 1691-1695, who assumed the
curvature of a rod to be proportional to the bending moment.
In 1772 Daniel Bernoulli (nephew of James) proposed in a letter to Leonhard
Euler that the potential energy of a bent rod is proportional to the square of
its curvature integrated over the length of the rod.
Euler, master in variation techniques, performed a thorough calculation of
the elastica in 1774. Both approaches are equivalent.
There are more problems related to the elastica. A nice survey can be found in the PhD thesis by Raph Levien
The elastica: A
mathematical history.
The closed curves are the shapes of buckled rings. They are elastica under homogeneous pressure from outside.
Lévy in 1884, Halphen in 1884-1888, and Greenhill in 1892-1899 investigated them.
A survey of these problems and solutions can be found in my paper
"From Elastica to floating bodies of equilibrium"
arXiv: 1909.12596
The Problems
Floating bodies of equilibrium in two dimensions
From 1935 to 1941 mathematicians at the university in Lviv (Ukraine, then
Lwów Poland, earlier Lemberg in Austria-Hungary), among them Stefan
Banach and Mark Kac, collected mathematical problems in a book, which became
known as the
Scottish Book, since they often
met in the Scottish Coffee House. Stanislaw Ulam posed the problem 19 of this
book: "Is a sphere the only solid of uniform density which will float in water
in any position?" The corresponding two-dimensional problem, which we address
here, reads: Are there long right cylindrical logs of
non-circular cross-section,
which can float in any position without tendency to rotate? In 1938
Herman Auerbach gave a large number of solutions for a solid of half the
density of water. Here we will mainly consider the case where the density is
different from 1/2. At the end I give a few examples for solutions to this
density 1/2.
A right cylinder is a body, which is bounded by two parallel, plane areas
(base and top areas) and a cylinder surface generated by parallel straight
lines, which are perpendicular to the base and top areas.
Tire track problem
This problem originated from the story "The Adventure of the Priory School" by
Arthur Conan Doyle, where Sherlock Holmes and Dr. Watson discuss in view of the
two tire tracks of a bicycle, which way the bicycle went. The problem is: Is it possible that tire tracks other then circles or straight lines
are created by bicyclists going in both directions? Then it is not
possible to determine which way the bicycle went. To solve this problem one
assumes a simplification (physicists often model systems by simplifications):
It is assumed that the steerer is perpendicular to the plane on which the
bicycle rides.
Electrons in a parabolic magnetic field
An electron moves in a plane in a magnetic field perpendicular to this
plane, where the magnetic field is parabolic, that is a constant plus some
other constant times the square of the distance from the origin. What are the
trajectories of the electron? Since the electron is only subject to the Lorentz
force, which is perpendicular to its velocity, the magnitude of the velocity is
constant, but its direction varies. The curvature of the trajectory is
proportional to the magnetic field strength.
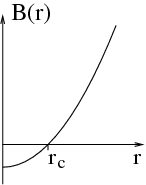 The magnetic field changes sign at rc. When the electron passes
through this distance from the origin, then the direction of the curvature of
the trajectory will change.
The magnetic field changes sign at rc. When the electron passes
through this distance from the origin, then the direction of the curvature of
the trajectory will change.
The Solution
There is a common solution to these problems. I do not give the mathematics
here. The interested reader will find it in the paper
physics/0701241. The solution involves double-periodic and related
Weierstrass-functions. In special cases which I will mention below, the result
can be expressed
by trigonometric and exponential functions. However, I will describe a few
properties of the solutions and I will show animated figures.
Floating bodies in equilibrium in two dimensions
Obviously the area of the cross-section below the water-line has to be the same
for any orientation of the log. It is given by the total cross-section
multiplied by the density of the body divided by the density of water
(Principle of Archimedes).
Discussion of the hydrostatic properties shows that the length of the water-line
(the line which separates the part of the cross-section below water from that
above water), which I denote by 2l, is constant. Moreover the length of
the boundary of the
cross-section below the water is also constant. In the animations the boundary
of the cross-section will be shown in black.
Instead of rotating the body, I will keep it fixed and assume that
the direction of gravitation is rotated. Then the various water-lines are shown
in
green and cyan. The red envelope of the water-lines touches in the middle. The
part inside the water-line is always above or below the water (provided inside
and outside is well defined, which is not the case, if the density of the solid
is half the density of water).
Tire track problem
With the simplification given above the distance between the points where the
front and the rear wheel touches the ground is constant. We denote it by
l. Then the end points of the tangent of length l to the
trace of the rear wheel in the direction of the movement of the bicycle yields
the trace of the front wheel. If the tangent lines in both directions end at
the trace of the front wheel, then it is open which way the bicycle went. Thus
we deal with the same problem as for the floating body. Now the black lines are
the traces of
the front wheel, the red lines the traces of the rear wheel, and the moving
green and cyan lines indicate the location of the bicycles at various times.
Property of constant chord length
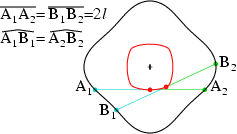
Thus we look for and find curves, which have the following property of
constant chord length: Starting from two appropriate points A1 and
A2 on the curve we move the same arbitrary length of the arc along
the curve to the points B1 and B2. Then the length of
the chord has to be the same A1A2 =
B1B2 = 2l.
On the solution
Originally I considered the floating body problem. I started with the circle,
which is an obvious solution. Then I distorted it slightly by allowing the
distance from the origin to oscillate so that going around the circle it was
periodically n times slightly larger, n times slightly less than the average
radius. One finds that this yields solutions for n-2 different densities. Then
I expanded the result in powers of this distortion (Taylor expansion) and I
realized, as far as I could perform the expansion, that the boundary was the
same for all n-2 different densities. It was necessary to perform extensive
algebraic calculations. Thus it was very useful to use computer algebra (Maple)
for this expansion. The assumption, that the boundary agreed for all densities,
made it possible to derive a differential equation for the boundary.
Electrons in a parabolic magnetic field
Integrating this differential equation once, one finds that the curvature of the
boundary depends quadratically on the radius. This, however, came only to my
mind after I had seen traces of electrons moving in a perpendicular linearly
increasing magnetic field, which were calculated by Evers, Mirlin, Polyakov,
and Wölfle, since they looked so similar to the curves I had determined in
the corresponding linear limit.
Different Conditions
The curves I will show in the following are solutions of a differential
equation, which contains several constants, which can be chosen to meet certain
conditions. In the case of the moving electrons there is no restriction.
In the
case of the bicyclist one will generally assume that he/she rides in one
direction; in particular that this applies for the rear wheel. If however,
he/she is very artistic and the bicycle allows, then there are also cases,
where he/she moves back and forth. For some solutions it would even be
necessary, that the steerer could be rotated by more than 180 degrees.
Nevertheless it may be that parts of the curve can be traversed without
problems. After all, bicyclists are not supposed to ride forever.
For the
boundary of the floating body one has to require that it is closed and the
cross-section is sufficiently convex so that the water-lines intersect the
boundary exactly twice, not more often.
Property of constant distance
The class of curves which are described here have the following remarkable
property: Choose two arbitrary points A'1 and A2 on the
black curve. Then there exists an angle δχ, by which the curve with
A2 is to be rotated into the blue curve, so that so that
A'1 is rotated to A1. If one moves from A1 and
A2 the same arbitrary length of the arc along the respective curves
to points I call B1 and B2, then the distance between
the points stays constant A1A2 =
B1B2 = 2l.
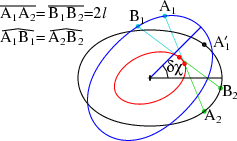
I call this the property of constant distance.
If A1 and A2 coincide, then the angle δχ equals
zero. It increases as the arc between the points A'1 and
A2 increases. Any time this angle δχ makes the black and
the blue curves coincide, one obtains a solution for chords of constant
length.
In the example with different rotation angles
δχ this is the case for δχ=900.
It is this property, which made it possible, to obtain a differential equation
for the curves by using it for an arbitrary small angle δχ.
(An animation for two rotating angles is shown below).
Branches and limit cases
Depending on the values of the constants in the differential equation one
obtains one branch of a curve or two branches. This should be not to
surprising, since something similar happens for conal sections. There one may
have
ellipses (one branch) or hyperbola (two branches) as solutions. One also
realizes that for conal sections one has certain limit cases. One such limit is
the
parabola (between ellipse and hyperbola), another one are two straight lines
(for a section through the vertex of the cone).
Similarly we have two special
limits here: One in which a circle is solution or asymptotically approached,
the other one is the linear limit, where most of the curves repeat periodically
in linear direction.
The shape of conal sections can be desribed by one number, which can be varied
continuously. For ellipses this can be the ratio between the two main axes.
(Generally the shape of a conal section is characterized by its numerical
eccentricity).
The shape of our curves is given by two numbers, which can be varied
continuously. Most of the curves repeat after rotations around a certain angle
ψr. Thus one of these numbers can be this angle. Here I will
mainly show figures which are closed. This is the case, if
ψr=3600×m/n with integer (coprime) m and n.
Thus the curve repeats after circling m times around the origin. During these m
revolutions the curve reaches n times its largest and also n times its smallest
distance from the center of the curve.
One needs m=1 for the floating body problem.
Another quantity, which can be varied is the ratio of the largest and the
smallest distance from the origin, which I will denote by
(1+ε)/(1-ε).
Threedimensional Bodies
The original problem read "Is a sphere the only solid of uniform density which
will float in water in any position?" Schneider and Falconer proved that the
only star-shaped central symmetric body which can float in all orientations at
density 1/2 is a sphere. A body is called star-shaped if there exists a point A
such that for each point P in the body the segment AP lies in the body.
By now I have performed two investigations to the problem of floating
threedimensional bodies. In both cases small deviations from the sphere are
considered:
In arxiv: 0803.1043 with
the title "Floating Bodies of Equilibrium in Three Dimensions. The central
symmetric case" the conditions for bodies with central symmetry and relative
density different from 1/2 are considered. It is, however, shown by an example
that there are central symmetric solutions at this density, if one skips the
requirement of star shape.
In arxiv: 0902.3538
with the title "Floating Bodies of Equilibrium at Density 1/2 in Arbitrary
Dimensions" it is shown that also in dimension three (and higher) there is a
large manifold of solutions for density 1/2. To any given envelope of the
water-surfaces, which has to have the property that there is only one tangent
at the envelope parallel to any given plane, there are solutions.
Presently I consider bodies, which are not central symmetric with densities
different from 1/2.
The Animations
As in the figures above the boundary of the floating body, the track of the
front tire, and the trajectory of the charge are depicted black and sometimes
blue. The water-line of the floating body is shown half in green, half in cyan.
The location of the two bicycles are given by the green and cyan lines. The
green and cyan endpoints move on the black (blue) curve and indicate the front
tires of the two bicycles. The
middle (red point) of this line generates the red envelope. It is the track of
the rear tire. The green and cyan end-points move in each step by
the same arc length along the black (blue) curve. The length l of
the green and cyan line stays constant.
Examples of boundaries for floating bodies
Here some solutions for
floating bodies with n=4, 5, and 6 are shown.
Note that in general a given shape of the body is solution for several
densities.
Of course these are also solutions to the tire track problem.
One may compare with the
examples given by David L. Finn.
Varying the ratio of the extremal radii
In order that the cross-sections of the floating bodies are sufficiently convex,
ε has to be sufficiently small. This applies also to the tire track
problem, since otherwise the bicyclist is forced to move back and forth with
the rear tire. In the figures for the floating bodies we had ε=0.1 for
n=4 and n=5, ε=0.05 for n=6.
Here we show figures for larger values of ε for
n=5.
If ε=1, then the curve goes through the origin. For larger
values of ε it passes the origin on the opposite side and the ratio of
largest and smallest distance from the origin is (1+ε)/(ε-1).
Property of constant distance
The property of constant distance mentioned above is
shown in two examples for m/n=1/2.
We remark that there is no solution for the chord of constant length, if n-m=1,
which is the case here.
m≠1 and the eight
m need not be 1. The first figure in m≠1, the eight
shows an example for m/n=2/5 with chord of constant length.
The other two figures show pairs of eights, which one obtains for m=0,
which are connected by lines of constant length. One has m/n=0/1 for these
eights. Thus there are no chords of constant length.
For reasons I will not explain here, also negative m can be used.
An example for m/n=-1/7 with three different lengths of
chords is shown.
Example with two branches
As mentioned before there may be two branches to a curve. Then it is not only
possible to have chords of constant length within any of these curves, but there
is also the property of constant distance between both curves. This is shown
for m/n=1/3, ε=3.0 in Threefold symmetry.
The degenerate case involving circles
In the following five web-sites curves are shown which can be constructed by
moving one (cyan) end of the straight line along a (magenta) circle in such away
that
the (red) middle of the line moves in the direction of the line, as if the line
were there borne by a wheel aligned in the direction of the line. The other
(green) end of the line describes the sought curve.
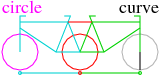
Here we use that the circle
is one of the two curves or that the curve approaches asymptotically the
circle. Thus we can use the property of constant distance between the circle
and the non trivial curve.
It should be emphasized that these solutions can be described by exponential and
trigonometric functions (see section 8 of the paper), whereas in the general
case double-periodic functions are needed.
In the following three websites the first figure shows this construction,
the second one the movement of the chord. These are no longer solutions to the
floating body problem, but the parts of the black and red curves which evade the
loops are solutions of the tire track problem.
ε is the ratio of the length of the line to the radius of the magenta
circle. If it is larger then two, then the black curves are periodic and three
εs were chosen which yield closed curves.
m/n=1/3, ε=5/2=2.5
m/n=-1/3, ε=sqrt(49/10)=2.213594
m/n=-2/1, ε=sqrt(64/15)=2.065591
If ε is less then two, then one obtains a curve inside and another one
outside the circle. In this case the curves approach asymptotically the magenta
circle. We show curves for ε=1.6.
In the limit case ε=2
one obtains one curve
approaching asymptotically the circle.
The linear Limit
One may let the extreme distances from the origin go to infinity, but keep their
differences finite. Then one obtains the linear limit case.
Again there are various possibilities. One may have
one branch of curve.
As long as the curves are so long stretched they are good solutions for the tire
track problem.
In the limit case of extreme stretching
there is no solution for a chord along the
same curve. However, there are such straight lines between two curves
transferred against each other.
The curve may also be generated by moving the cyan end of our line of length
2l along the magenta straight line so that the middle runs parallel to
itself. Then the green end traverses the black curve.
In the linear limit one may also have two branches
of curves.
Between them there are straight lines of constant length with arbitrarily many
lengths.
These types of curves have appeared in a paper by
Evers, Mirlin, Polyakov, and
Wölfle (see figs. 1 and 2) as trajectories of electrons in a magnetic
field perpendicular to the plane, which increases linearly in one direction of
the plane.
The carousels by Oliveros, Montejano and Bracho
Oliveros, Montejano and Bracho introduce dynamical equilateral (but not
equiangular) pentagons, whose vertices run on one or five equal curves, where
their edges constitute chords or line segments of constant length. (They call
these 'carousels'.)
In the carousels I the vertices of the
pentagon run along five eights and along closed curves with m/n=1/7 and 1/12.
The area of the pentagon stays constant.
In the carousels II five copies of a curve with
ε=1 are shown, which are rotated against each other by two
different angles supporting the vertices of the pentagon. In addition a set of
five identical curves of the linear case is shown, along which the pentagon
crawls. If the pentagon
intersects, then the difference of the two areas is constant.
Solutions for density 1/2
In 1938 Auerbach gave the general solution for density 1/2.
Then the envelope has to have the property that there is only one
tangente to each direction and that it closes after the direction of the
tangent has been rotated by 1800.
In general such an envelope has an odd number of cusps.
It may consist for example out of arcs.
These envelopes may degenerate to
polygons. One with five vertices is a pentagram.
The boundaries need not have corners. One of
Auerbach's examples has the shape of a heart.
The other one is without corners. The examples consist of two or three straight
lines and the same number of curves lines vis-a-vis.
These are pieces of the lines, which already appeared above as the limit case of
extreme stretching.
Here are further examples without corners..
In general the solutions for density 1/2 are no longer solutions for the
trajectories of electrons in a parabolic magnetic field. They are still
solutions to the tire track problem, if the cyclist is able to go back and
forth in an artistic way.
Back to the beginning
 The magnetic field changes sign at rc. When the electron passes
through this distance from the origin, then the direction of the curvature of
the trajectory will change.
The magnetic field changes sign at rc. When the electron passes
through this distance from the origin, then the direction of the curvature of
the trajectory will change.


