|
|
Stochastic dynamics of adhesion clusters
|
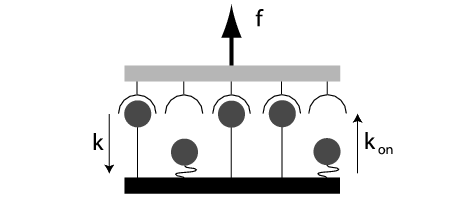
| Simple generic model for an adhesion cluster: two opposing and mechanically loaded surfaces are held together by an arrangement of parallel adhesion bonds. Each closed bond can dissociate with a force-dependent rate while each open bond can rebind with a constant rate. Load sharing leads to cooperativity and threshold behaviour in the cluster. |
One of the central challenges of a multicellular organism is to reconsile the conflicting requirements of holding together the cells and allowing for dynamic rearrangements in response to perturbations, e.g. when a wound has been inflicted. Multicellularity itself holds the key to this dilemma: while some cells ensure adhesive stability, others move and change things. However, the respective division of labor is not fixed, but there is a continuous change in the way different cells contribute to these two important tasks. Most importantly, these conflicting requirements also have to be realized on the level of single adhesion clusters. Indeed, all adhesion bonds have a relatively short lifetime, thus ensuring that the system is sufficiently dynamic to react to changes. At the same time, stability is guaranteed by continuous formation of new bonds. In many cases, this is simply rebinding of broken bonds. Short lifetimes correspond to small bond energies, which are of the order of thermal energy. This implies that thermal energy from the environment is sufficient to break adhesion bonds. The thermally activated nature of the rupture means that bond rupture is intrinsically stochastic, as indeed confirmed by dynamic force spectroscopy.
Dissociation of adhesion bonds is further increased by forces acting across the adhesion, a situation which is generic in multicellular organisms. For example, most tissue cell types are contractile, putting their cell-cell and cell-matrix under large mechanical load. Forces at adhesion contacts also arise from external sources like blood flow and muscle contraction in the body. From a physical point of view, force leads to a decrease in bond lifetime and therefore destabilizes adhesion. In order to cope with this problem, biological systems have evolved many ways to counteract the disruptive effect of force. Instead of letting force dissociate the system, in many instances force triggers a stabilization response. On the molecular level, this can be achieved for example by catch bonds, which are molecules with an complex internal structure, effectively leading to less dissociation under increased force. Catch bonding has been observed for several molecular systems, including P-selectin involved in rolling adhesion. On the subcellular level, force-induced growth of adhesion clusters has been reported both for focal contacts and adherens junctions.
In order to understand these biological phenomena, it is important to work out the underlying physical principles of force-induced dissociation and its interplay with rebinding in simple model systems. In order to investigate the effect of force on adhesion clusters, we introduced a one-step Master equation which describes the stochastic dynamics of a cluster of N0 parallel bonds under dimensionless force f and with dimensionless rebinding rate g (Physical Review Letters 2004, Journal of Chemical Physics 2004). Force is assumed to be shared equally between all i closed bonds (with i ranging from 0 to N0). Since bond rupture is a thermally activated process, the single bond dissociation rate is assumed to be exp(f/i). The single bond association rate g is assumed to be force-independent. Since the cluster usually cannot rebind from the completely dissociated state (i=0) due to elastic recoil of the transducer, it is treated as an absorbing boundary. Our model has three parameters (N0, f and g) and can be solved exactly only in a few special cases (like g = 0). In the general case, we solve the model by exact stochastic simulations (Gillespie algorithm). However, if one is interested only in the mean cluster lifetime, exact results can be found for the general case. We find that in order to increase cluster lifetime, increasing rebinding rate g is much more efficient than increasing cluster size N0. Force destabilizes the cluster, but this effect becomes considerably stronger above a threshold in force.
Experimentally, it is very difficult to measure the rebinding rate g. However, combining our exact results and experimental results for cluster lifetime, now one can estimate this important quantity. Our results can also be applied to situations in cell adhesion which occur on such a fast time scale that cluster stability is not increased by reenforcement processes (like rolling adhesion of white blood cells). Our results do not apply directly to focal adhesions, which grow rather than decay under force. However, our model suggest that if cytoskeletal loading is regulated to be close to the threshold in force, a small increase in motor activity can lead to strongly increased forces on single bonds, possibly triggering the reenforcement processes typical for focal adhesions. Finally, our model can be applied to dynamic force spectroscopy, in which case one usually deals with linearly rising rather than constant force (Europhysics Letters 2004). By including the effect of separation in the rebinding process, we also were able to predict that small adhesion clusters should be characterized by bistability, that is there should be stochastic switching between bound and unbound states (Biophysical Journal 2006, European Physics Journal E 2007).
We also collaborate with experimental groups on analyzing data from dynamic force spectroscopy and single-cell force spectroscopy. We have used our master equation approach to extract the mean number of initially closed bonds in biomembrane force probe experiments (Europhysics Letters 2008). For single-cell force spectroscopy, this approach has to be supplemented by mechanical models for cells (European Journal of Physiology 2008).
Recently we have generalized our modeling approach to the case of specific adhesion between sliding surfaces. This situation occurs for example at the interface between retrograde flow and the substrate, which is believed to be used by cells as a clutch regulating how strongly the moving edge protrudes during cell migration. Our work shows a biphasic relation between flow velocity and traction force, and identifies a regime of stick-slip motion. Both phenomena agree well with recent experimental results and are well known from the physics of sliding friction, but have not been studied much before in the context of cell adhesion (Journal of Physics Condensed Matter 2010).
Published work:
- T. Erdmann and U. S. Schwarz, Stability of adhesion clusters under constant force, Phys. Rev. Lett. 92: 108102 (2004) (abstract, cond-mat/0401533, DOI: 10.1103/PhysRevLett.92.108102, PDF)
- T. Erdmann and U. S. Schwarz, Adhesion clusters under shared linear loading: a stochastic analysis, Europhys. Lett. 66: 603-609 (2004) (abstract, cond-mat/0403552, DOI: 10.1209/epl/i2003-10239-3, PDF)
- T. Erdmann and U. S. Schwarz, Stochastic dynamics of adhesion clusters under shared constant force and with rebinding, J. Chem. Phys. 121: 8997-9017 (2004) (abstract, cond-mat/0405247, DOI: 10.1063/1.1805496, PDF)
- T. Erdmann and U.S. Schwarz. Bistability of cell-matrix adhesions resulting from non-linear receptor-ligand dynamics. Biophys. J., 91: L60-L62 (2006) (abstract, q-bio.SC/0608007, doi:10.1529/biophysj.106.090209, PDF)
- T. Erdmann and U. S. Schwarz. Impact of receptor-ligand distance on adhesion cluster stability. Eur. Phys. J. E, 22:123-137, 2007. (abstract, cond-mat/0612457v2, doi:10.1140/epje/e2007-00019-8, PDF)
- T. Erdmann, S. Pierrat, P. Nassoy, and U.S. Schwarz. Dynamic force spectroscopy on multiple bonds: experiments and model. Europhys. Lett., 81:48001, 2008. (abstract, qbio arXiv:0712.3042, PDF)
- T. Ludwig, R. Kirmse, K. Poole, and U.S. Schwarz. Probing cellular microenvironments and tissue remodelling by atomic force microscopy. Pflugers Arch - Eur J Physiol, 456:29-49, 2008. (abstract, doi:10.1007/s00424-007-0398-9, PDF)
- B. Sabass and U. S. Schwarz. Modelling cytoskeletal flow over adhesion sites: competition between stochastic bond dynamics and intracellular relaxation. J. Phys. Condensed Matter, 22:194112, 2010. (doi:10.1088/0953-8984/22/19/194112, PDF)
Last modified Thu Oct 16 17:25:46 CEST 2008
by USS.
Back to home page Ulrich Schwarz.